Proposition I.5
The base angles of an isosceles triangle are equal
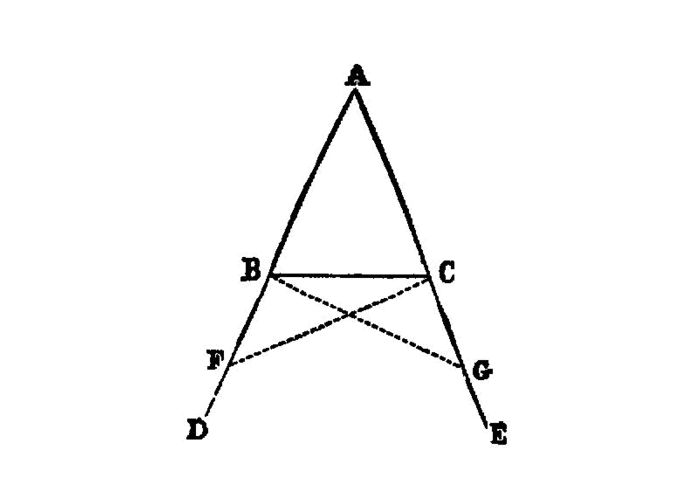
In isosceles triangles the angles at the base are equal to one another, and, if the equal straight 1 lines be produced further, the angles under the base will be equal to one another.
Let ABC be an isosceles triangle having the side AB equal to the side AC; and let the straight lines BD, CE be produced further in a straight line with AB, AC. I.post.2
I say that the angle ABC is equal to the angle ACB, and the angle CBD to the angle BCE.
Let a point F be taken at random on BD; 2 from AE the greater let AG be cut off equal to AF the less; I.3 and let the straight lines FC, GB be joined. I.post.1
Then, since AF is equal to AG and AB to AC,
- the two sides
FA,ACare equal to the two sidesGA,AB, respectively; 3
and they contain a common angle, the angle FAG.
- Therefore the base
FCis equal to the baseGB, and the triangleAFCis equal to the triangleAGB,
and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend,
- that is, the angle
ACFto the angleABG, and the angleAFCto the angleAGB. [I.4]
And, since the whole AF is equal to the whole AG,
- and in these
ABis equal toAC, the remainderBFis equal to the remainderCG.
But FC was also proved equal to GB; therefore the two sides BF, FC are equal to the two sides CG, GB respectively; and the angle BFC is equal to the angle CGB,
- while the base
BCis common to them; 4
therefore the triangle BFC is also equal to the triangle CGB, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend;
- therefore the angle
FBCis equal to the angleGCB, and the angleBCFto the angleCBG.
Accordingly, since the whole angle ABG was proved equal to the angle ACF,
- and in these the angle
CBGis equal to the angleBCF,
the remaining angle ABC is equal to the remaining angle ACB;
- and they are at the base of the triangle
ABC.
But the angle FBC was also proved equal to the angle GCB;
- and they are under the base.
Therefore etc.
- Q. E. D. 5
References
Footnotes
-
the equal straight lines
(meaning the equal sides). Cf. note on the similar expression in Prop. 4, lines 2, 3. ↩ -
Let a point F be taken at random on BD
,εἰλήφθω ἐπὶ τῆς ΒΔ τυχὸν σημεῖον τὸ Ζ , whereτυχὸν σημεῖον meansa chance point.
↩ -
the two sides FA, AC are equal to the two sides GA, AB respectively,
δύο αἱ ΖΑ, ΑΓ δυσὶ ταῖς ΗΑ, ΑΒ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ -
the base BC is common to them,
i.e., apparently, common to the angles, as theαὐτῶν inβάσις αὐτῶν κοινὴ can only refer toγωνία andγωνίᾳ preceding. Simson wroteand the base
; Todhunter left out these words as being of no use and tending to perplex a beginner. But Euclid evidently chose to quote the conclusion of I. 4 exactly; the first phrase of that conclusion is that the bases (of the two triangles) are equal, and, as the equal bases are here the same base, Euclid naturally substitutes the wordBCis common to the two trianglesBFC,CGBcommon
forequal.
↩ -
Q.E.D.
As(Being) what it was required to prove
(ordo
) is somewhat long, I shall henceforth write the time-honouredQ. E. D.
andQ. E. F.
forὅπερ ἔδει δεῖξαι andὅπερ ἔδει ποιῆσαι . ↩
