Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute angled triangle that which has its three angles acute.

On a given finite straight line ¹ to construct an equilateral triangle.

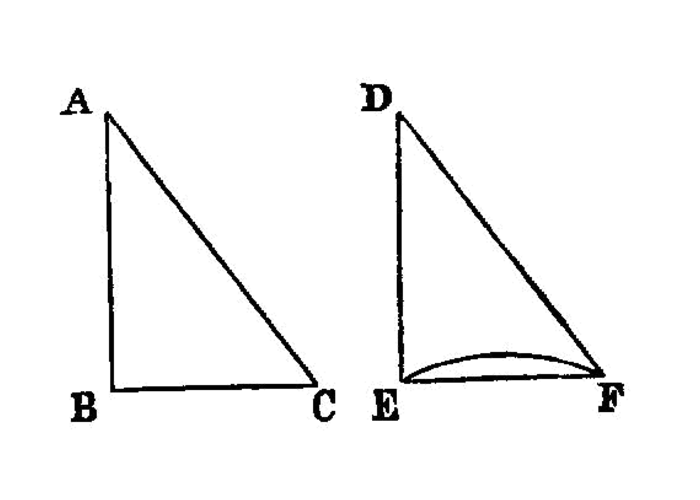
If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base ¹ equal to the base, the triangle will be equal to the triangle, and the remaining angles ² will be equal to the remaining angles respectively, ³ namely those which the equal sides subtend. ⁴

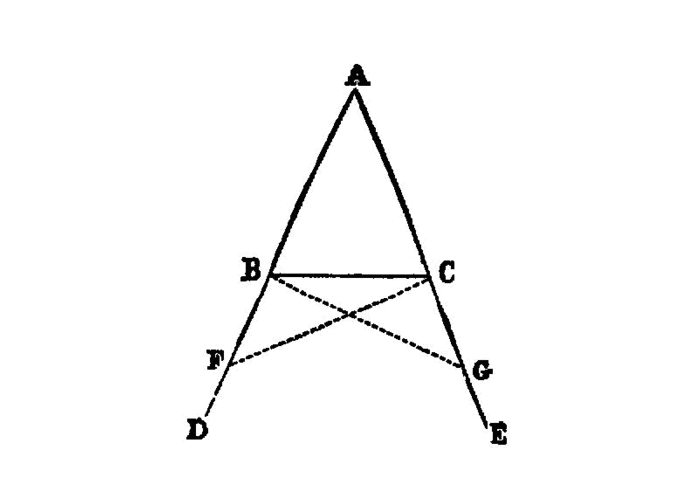
In isosceles triangles the angles at the base are equal to one another, and, if the equal straight ¹ lines be produced further, the angles under the base will be equal to one another.