Proposition I.1

Construct an Equilateral Triangle on a Segment

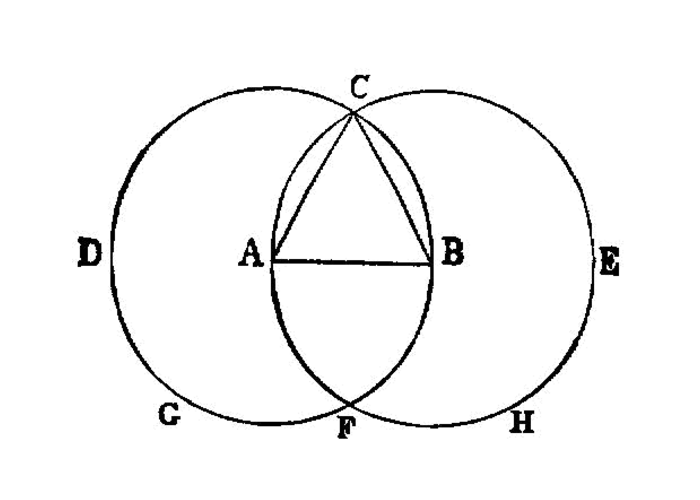
On a given finite straight line 1 to construct an equilateral triangle.

Let AB be the given finite straight line.2

Thus it is required to construct an equilateral triangle on the straight line AB.

With centre A and distance AB let the circle BCD be described3; I.post.3 again, with centre B and distance BA let the circle ACE be described; I.post.3 and from the point C4, in which the circles cut one another, to the points A, B let the straight lines CA, CB be joined. I.post.1

Now, since the point A is the centre of the circle CDB,

Again, since the point B is the centre of the circle CAE,

But CA was also proved equal to AB; therefore each of the straight lines CA, CB is equal to AB.

And things which are equal to the same thing are also equal to one another; I.c.n.1

  • therefore CA is also equal to CB.

Therefore the three straight lines CA, AB, BC are equal to one another.5

Therefore the triangle ABC is equilateral; and it has been constructed on the given finite straight line AB.

  • (Being) what it was required to do.

References

graph BT I_1[ I.1 ]:::post; %%%% I_1 dependencies I_post1( I.post.1 ):::post; click I_post1 "/elem.1.post.1" "Book I Postulate 1"; I_post3( I.post.3 ):::post click I_post3 "/elem.1.post.3" "Book I Postulate 3"; I_def15( I.def.15 ):::def click I_def15 "/elem.1.def.15" "Book I Definition 15"; I_cn1( I.c.n.1 ):::cn click I_cn1 "/elem.1.c.n.1" "Book I Common Notion 1"; %%%% I_1 links I_1 --> I_post1 I_1 --> I_post3 I_1 --> I_def15 I_1 --> I_cn1

Footnotes

  1. On a given finite straight line
    The Greek usage differs from ours in that the definite article is employed in such a phrase as this where we have the indefinite. ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης, on the given finite straight line, i.e. the finite straight line which we choose to take. ↩

  2. Let AB be the given finite straight line.
    To be strictly literal we should have to translate in the reverse order let the given finite straight line be the (straight line) AB ; but this order is inconvenient in other cases where there is more than one datum, e.g. in the setting-out of I. 2, let the given point be A, and the given straight line BC, the awkwardness arising from the omission of the verb in the second clause. Hence I have, for clearness' sake, adopted the other order throughout the book. ↩

  3. let the circle BCD be described.
    Two things are here to be quoted,

    1. the elegant and practically universal use of the perfect passive imperative in constructions, γεγράφθω meaning of course let it have been described or suppose it described,
    2. the impossibility of expressing shortly in a translation the force of the words in their original order. κύκλος γεγράφθω ὸ ΒΓΔ means literally let a circle have been described, the (circle, namely, which I dequote by) BCD. Similarly we have lower down let straight lines, (namely) the (straight lines) CA, CB, be joined, ἐπεζεύχθωσαν εὐθεῖαι αί ΓΑ, ΓΒ. There seems to be no practicable alternative, in English, but to translate as I have done in the text.

    ↩

  4. from the point C
    Euclid is careful to adhere to the phraseology of Postulate 1 except that he speaks of joining (ἐπεζεύχθωσαν) instead of drawing (γράφειν). He does not allow himself to use the shortened expression let the straight line FC be joined (without mention of the points F, C) until I. 5. ↩

  5. each of the straight lines CA, CB
    , ἑκατέρα τῶν ΓΑ, ΓΒ and 24. the three straight lines CA, AB, BC, αἱ τρεῖς αἱ ΓΑ, ΑΒ, ΒΓ. I have, here and in all similar expressions, inserted the words straight lines which are not in the Greek. The possession of the inflected definite article enables the Greek to omit the words, but this is not possible in English, and it would scarcely be English to write each of CA, CB or the three CA, AB, BC. ↩