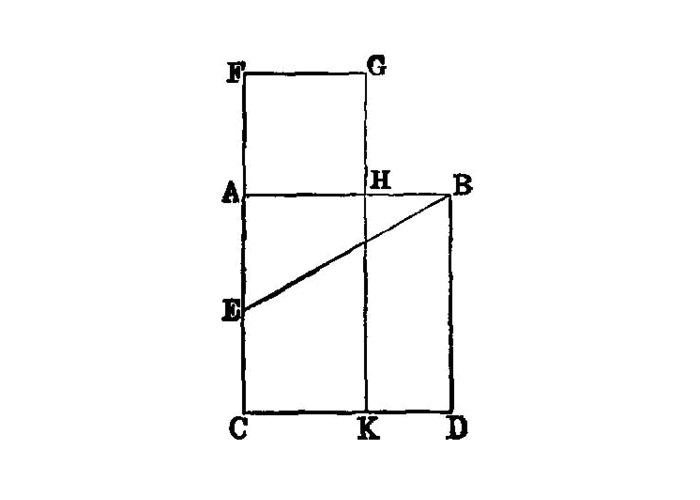
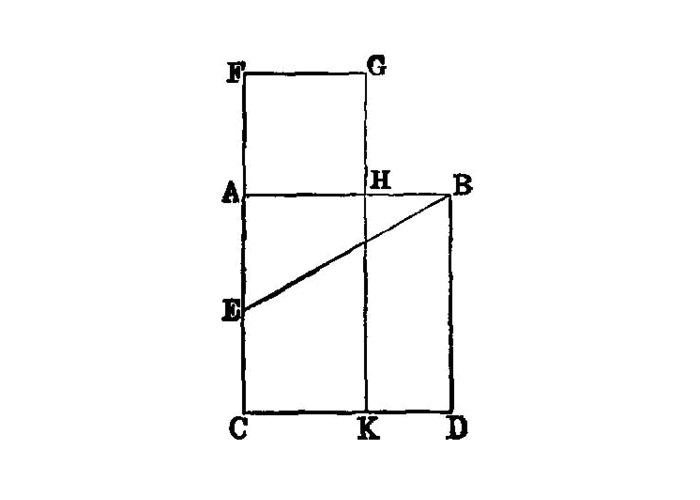
To cut a given straight line so that the rectangle contained by the whole and one of the segments is equal to the square on the remaining segment.

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.

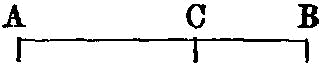
To cut a given finite straight line in extreme and mean ratio.

If a straight line be cut in extreme and mean ratio, the square on the greater segment added to the half of the whole is five times the square on the half.

If the square on a straight line be five times the square on a segment of it, then, when the double of the said segment is cut in extreme and mean ratio, the greater segment is the remaining part of the original straight line.

If a straight line be cut in extreme and mean ratio, the square on the lesser segment added to the half of the greater segment is five times the square on the half of the greater segment.

If a straight line be cut in extreme and mean ratio, the square on the whole and the square on the lesser segment together are triple of the square on the greater segment.

If a straight line be cut in extreme and mean ratio, and there be added to it a straight line equal to the greater segment, the whole straight line has been cut in extreme and mean ratio, and the original straight line is the greater segment.

If a rational straight line be cut in extreme and mean ratio

If in an equilateral and equiangular pentagon straight lines subtend two angles taken in order, they cut one another in extreme and mean ratio, and their greater segments are equal to the side of the pentagon.

If the side of the hexagon and that of the decagon inscribed in the same circle be added together, the whole straight line has been cut in extreme and mean ratio, and its greater segment is the side of the hexagon.

If in a circle which has its diameter rational an equilateral pentagon be inscribed, the side of the pentagon is the irrational straight line called minor.

To construct an icosahedron and comprehend it in a sphere, like the aforesaid figures; and to prove that the side of the icosahedron is the irrational straight line called minor.

To construct a dodecahedron and comprehend it in a sphere, like the aforesaid figures, and to prove that the side of the dodecahedron is the irrational straight line called apotome.

To set out the sides of the five figures and to compare them with one another.