Proposition I.2

Construct equal segments by extension

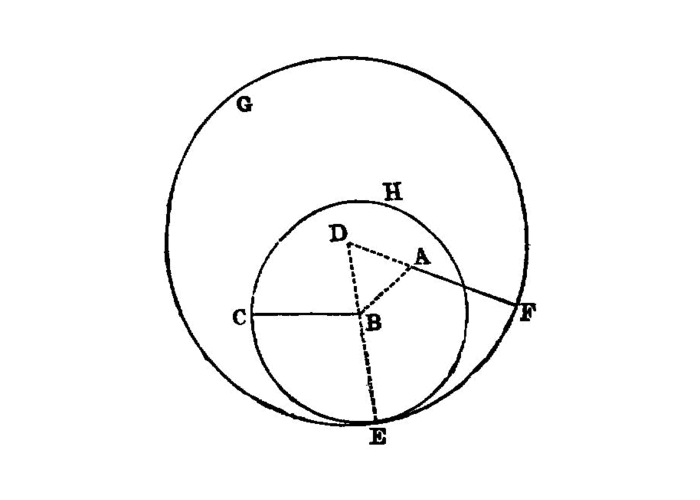
To place at a given point (as an extremity) a straight line equal to a given straight line.

Let A be the given point, and BC the given straight line.

Thus it is required to place at the point A (as an extremity)1 a straight line equal to the given straight line BC.

From the point A to the point B let the straight line AB be joined; I.post.1 and on it let the equilateral triangle DAB be constructed. I.1

Let the straight lines AE, BF be produced2 in a straight line with DA, DB; I.post.2 with centre B and distance BC let the circle CGH be described; I.post.3 and again, with centre D and distance DG let the circle GKL be described. I.post.3

Then, since the point B is the centre of the circle CGH,

  • BC is equal to BG.

Again, since the point D is the centre of the circle GKL,

  • DL is equal to DG.

And in these DA is equal to DB;

  • therefore the remainder AL is equal to the remainder BG3. I.c.n.3

But BC was also proved equal to BG;

  • therefore each of the straight lines AL, BC is equal to BG.

And things which are equal to the same thing are also equal to one another; I.c.n.1

  • therefore AL is also equal to BC.

Therefore at the given point A the straight line AL is placed equal to the given straight line BC.

  • (Being) what it was required to do.

References

graph BT I_2[ I.2 ]:::prop; click I_2 "/elem.1.2" "Book I Proposition 2"; %%%% I_2 dependencies I_1[ I.1 ]:::prop; click I_1 "/elem.1.1" "Book I Proposition 1"; I_post1( I.post.1 ):::post; click I_post1 "/elem.1.post.1" "Book I Postulate 1"; I_post2( I.post.2 ):::post; click I_post2 "/elem.1.post.2" "Book I Postulate 2"; I_post3( I.post.3 ):::post; click I_post3 "/elem.1.post.3" "Book I Postulate 3"; I_def15( I.def.15 ):::def; click I_def15 "/elem.1.def.15" "Book I Definition 15"; %%%% I_2 links I_2 --> I_1 I_2 --> I_post1 I_2 --> I_post2 I_2 --> I_post3 I_2 --> I_def15 %%%% I_1 dependencies I_post1( I.post.1 ):::post; click I_post1 "/elem.1.post.1" "Book I Postulate 1"; I_post3( I.post.3 ):::post click I_post3 "/elem.1.post.3" "Book I Postulate 3"; I_def15( I.def.15 ):::def click I_def15 "/elem.1.def.15" "Book I Definition 15"; I_cn1( I.c.n.1 ):::cn click I_cn1 "/elem.1.c.n.1" "Book I Common Notion 1"; %%%% I_1 links I_1 --> I_post1 I_1 --> I_post3 I_1 --> I_def15 I_1 --> I_cn1

Footnotes

  1. (as an extremity).
    I have inserted these words because to place a straight line at a given point (πρὸς τῷ δοθέντι σημείῳ) is not quite clear enough, at least in English. ↩

  2. Let the straight lines AE, BF be produced....
    It will be observed that in this first application of Postulate 2, and again in I. 5, Euclid speaks of the continuation of the straight line as that which is produced in such cases, ἐκβεβλήσθωσαν and προσεκβεβλήσθωσαν meaning little more than drawing straight lines in a straight line with the given straight lines. The first place in which Euclid uses phraseology exactly corresponding to ours when speaking of a straight line being produced is in I. 16: let one side of it, BC, be produced to D (προσεκβεβλήσθω αὐτοῦ μία πλευρὰ ἡ ΒΓ ἐπὶ τὸ Δ). ↩

  3. the remainder AL...the remainder BG.
    The Greek expressions are λοιπὴ ἡ ΑΛ and λοιπῇ τῇ BH, and the literal translation would be AL (or BG) remaining, but the shade of meaning conveyed by the position of the definite article can hardly be expressed in English. ↩