Proposition I.32
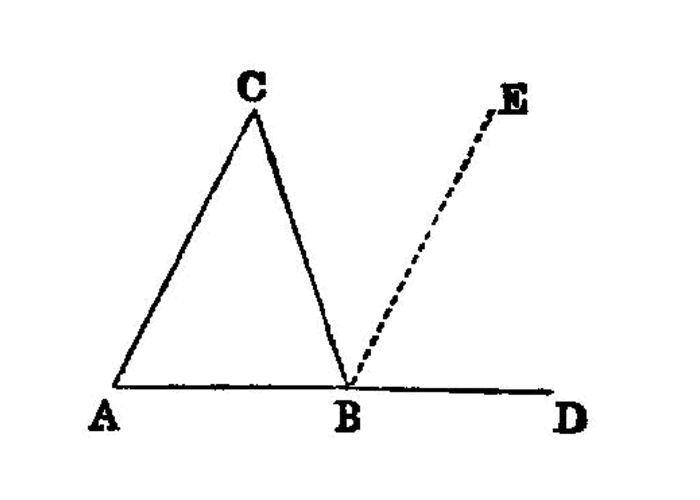
In any triangle, if one of the sides be produced, the exterior angle is equal to the two interior and opposite angles, and the three interior angles of the triangle are equal to two right angles.
Let ABC be a triangle, and let one side of it BC be produced to D;
I say that the exterior angle ACD is equal to the two interior and opposite angles CAB, ABC, and the three interior angles of the triangle ABC, BCA, CAB are equal to two right angles.
For let CE be drawn through the point C parallel to the straight line AB. I.31
Then, since AB is parallel to CE,
- and
AChas fallen upon them, the alternate anglesBAC,ACEare equal to one another. I.29
Again, since AB is parallel to CE,
- and the straight line
BDhas fallen upon them,
the exterior angle ECD is equal to the interior and opposite angle ABC. I.29
But the angle ACE was also proved equal to the angle BAC;
- therefore the whole angle
ACDis equal to the two interior and opposite anglesBAC,ABC.
Let the angle ACB be added to each;
- therefore the angles
ACD,ACBare equal to the three anglesABC,BCA,CAB.
But the angles ACD, ACB are equal to two right angles; I.13
- therefore the angles
ABC,BCA,CABare also equal to two right angles.
Therefore etc.
- Q. E. D.
