Proposition 11.4
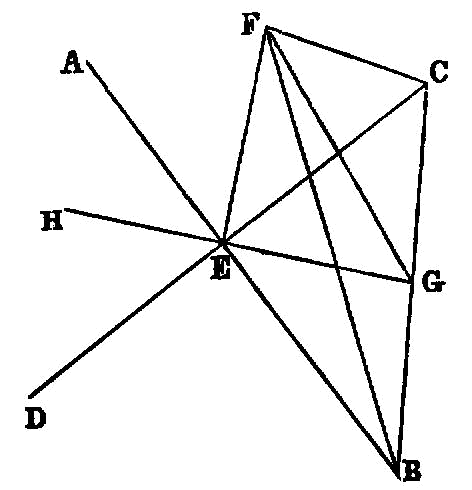
If a straight line be set up at right angles to two straight lines which cut one another, at their common point of section, it will also be at right angles to the plane through them.
If a straight line be set up at right angles to two straight lines which cut one another, at their common point of section, it will also be at right angles to the plane through them.
For let a straight line EF be set up at right angles to the two straight lines AB, CD, which cut one another at the point E, from E; I say that EF is also at right angles to the plane through AB, CD.
For let AE, EB, CE, ED be cut off equal to one another, and let any straight line GEH be drawn across through E, at random; let AD, CB be joined, and further let FA, FG, FD, FC, FH, FB be joined from the point F taken at random <on EF>.
Now, since the two straight lines AE, ED are equal to the two straight lines CE, EB, and contain equal angles, [I. 15] therefore the base AD is equal to the base CB, and the triangle AED will be equal to the triangle CEB; [I. 4] so that the angle DAE is also equal to the angle EBC.
But the angle AEG is also equal to the angle BEH; [I. 15] therefore AGE, BEH are two triangles which have two angles equal to two angles respectively, and one side equal to one side, namely that adjacent to the equal angles, that is to say, AE to EB; therefore they will also have the remaining sides equal to the remaining sides. [I. 26]
Therefore GE is equal to EH, and AG to BH.
And, since AE is equal to EB, while FE is common and at right angles, therefore the base FA is equal to the base FB. [I. 4]
For the same reason FC is also equal to FD.
And, since AD is equal to CB, and FA is also equal to FB, the two sides FA, AD are equal to the two sides FB, BC respectively; and the base FD was proved equal to the base FC; therefore the angle FAD is also equal to the angle FBC. [I. 8]
And since, again, AG was proved equal to BH, and further FA also equal to FB, the two sides FA, AG are equal to the two sides FB, BH.
And the angle FAG was proved equal to the angle FBH; therefore the base FG is equal to the base FH. [I. 4]
Now since, again, GE was proved equal to EH, and EF is common, the two sides GE, EF are equal to the two sides HE, EF; and the base FG is equal to the base FH; therefore the angle GEF is equal to the angle HEF. [I. 8]
Therefore each of the angles GEF, HEF is right.
Therefore FE is at right angles to GH drawn at random through E.
Similarly we can prove that FE will also make right angles with all the straight lines which meet it and are in the plane of reference.
But a straight line is at right angles to a plane when it makes right angles with all the straight lines which meet it and are in that same plane; [XI. Def. 3] therefore FE is at right angles to the plane of reference.
But the plane of reference is the plane through the straight lines AB, CD.
Therefore FE is at right angles to the plane through AB, CD.
Therefore etc. Q. E. D.
