Proposition 3.33
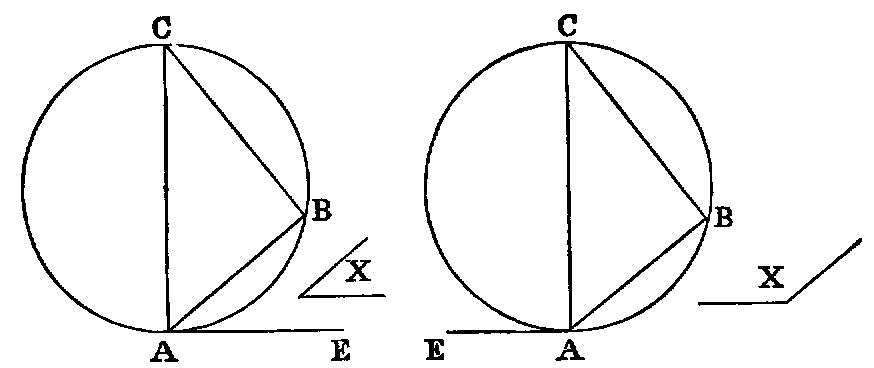
On a given straight line to describe a segment of a circle admitting an angle equal to a given rectilineal angle.
Let AB be the given straight line, and the angle at C the given rectilineal angle; thus it is required to describe on the given straight line AB a segment of a circle admitting an angle equal to the angle at C.
The angle at C is then acute, or right, or obtuse.
First let it be acute, and, as in the first figure, on the straight line AB, and at the point A, let the angle BAD be constructed equal to the angle at C; therefore the angle BAD is also acute.
Let AE be drawn at right angles to DA, let AB be
Then, since AF is equal to FB, and FG is common, the two sides AF, FG are equal to the two sides BF, FG; and the angle AFG is equal to the angle BFG; therefore the base AG is equal to the base BG. [I. 4]
Therefore the circle described with centre G and distance GA will pass through B also.
Let it be drawn, and let it be ABE; let EB be joined.
Now, since AD is drawn from A, the extremity of the diameter AE, at right angles to AE, therefore AD touches the circle ABE. [III. 16, Por.]
Since then a straight line AD touches the circle ABE, and from the point of contact at A a straight line AB is drawn across in the circle ABE, the angle DAB is equal to the angle AEB in the alternate segment of the circle. [III. 32]
But the angle DAB is equal to the angle at C; therefore the angle at C is also equal to the angle AEB.
Therefore on the given straight line AB the segment AEB of a circle has been described admitting the angle AEB equal to the given angle, the angle at C.
Next let the angle at C be right; and let it be again required to describe on AB a segment of a circle admitting an angle equal to the right angle at C.
Let the angle BAD be constructed equal to the right angle at C, as is the case in the second figure;
Therefore the straight line AD touches the circle ABE, because the angle at A is right. [III. 16, Por.]
And the angle BAD is equal to the angle in the segment AEB, for the latter too is itself a right angle, being an angle in a semicircle. [III. 31]
But the angle BAD is also equal to the angle at C.
Therefore the angle AEB is also equal to the angle at C.
Therefore again the segment AEB of a circle has been described on AB admitting an angle equal to the angle at C.
Next, let the angle at C be obtuse; and on the straight line AB, and at the point A, let the angle BAD be constructed equal to it, as is the case in the third figure; let AE be drawn at right angles to AD, let AB be again bisected at F, let FG be drawn at right angles to AB, and let GB be joined.
Then, since AF is again equal to FB, and FG is common, the two sides AF, FG are equal to the two sides BF, FG; and the angle AFG is equal to the angle BFG; therefore the base AG is equal to the base BG. [I. 4]
Therefore the circle described with centre G and distance GA will pass through B also; let it so pass, as AEB.
Now, since AD is drawn at right angles to the diameter AE from its extremity, AD touches the circle AEB. [III. 16, Por.]
And AB has been drawn across from the point of contact at A; therefore the angle BAD is equal to the angle constructed in the alternate segment AHB of the circle. [III. 32]
But the angle BAD is equal to the angle at C.
Therefore the angle in the segment AHB is also equal to the angle at C.
Therefore on the given straight line AB the segment AHB of a circle has been described admitting an angle equal to the angle at C. Q. E. F.
