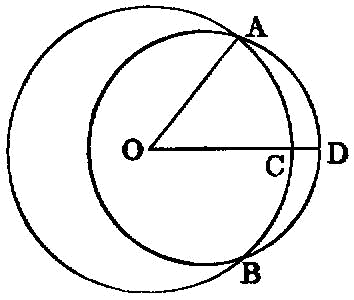
If two circles cut one another, they will not have the same centre.

For let the circles ABC, CDG cut one another at the points B, C; I say that they will not have the same centre.

For, if possible, let it be E; let EC be joined, and let EFG be drawn through at random.

Then, since the point E is the centre of the circle ABC, EC is equal to EF. [I. Def. 15]

Again, since the point E is the centre of the circle CDG, EC is equal to EG.

But EC was proved equal to EF also; therefore EF is also equal to EG, the less to the greater : which is impossible.

Therefore the point E is not the centre of the circles ABC, CDG.

Therefore etc. Q. E. D.