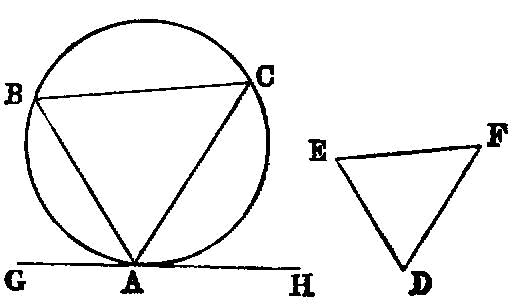
In a given circle to inscribe a triangle equiangular with a given triangle.

Let ABC be the given circle, and DEF the given triangle; thus it is required to inscribe in the circle ABC a triangle equiangular with the triangle DEF.

Let GH be drawn touching the circle ABC at A [III. 16, Por.]; on the straight line AH, and at the point A on it, let the angle HAC be constructed equal to the angle DEF, and on the straight line AG, and at the point A on it, let the angle GAB be constructed equal to the angle DFE; [I. 23] let BC be joined.

Then, since a straight line AH touches the circle ABC, and from the point of contact at A the straight line AC is drawn across in the circle, therefore the angle HAC is equal to the angle ABC in the alternate segment of the circle. [III. 32]

But the angle HAC is equal to the angle DEF; therefore the angle ABC is also equal to the angle DEF.

For the same reason the angle ACB is also equal to the angle DFE; therefore the remaining angle BAC is also equal to the remaining angle EDF. [I. 32]

Therefore in the given circle there has been inscribed a triangle equiangular with the given triangle. Q. E. F.