Proposition 6.17
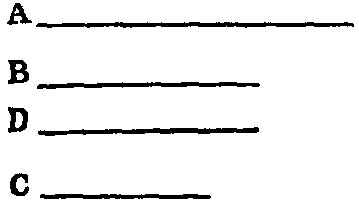
If three straight lines be proportional, the rectangle contained by the extremes is equal to the square on the mean; and, if the rectangle contained by the extremes be equal to the square on the mean, the three straight lines will be proportional.
Let the three straight lines A, B, C be proportional, so that, as A is to B, so is B to C; I say that the rectangle contained by A, C is equal to the square on B.
Let D be made equal to B.
Then, since, as A is to B, so is B to C, and B is equal to D, therefore, as A is to B, so is D to C.
But, if four straight lines be proportional, the rectangle contained by the extremes is equal to the rectangle contained by the means. [VI. 16]
Therefore the rectangle A, C is equal to the rectangle B, D.
But the rectangle B, D is the square on B, for B is equal to D; therefore the rectangle contained by A, C is equal to the square on B.
Next, let the rectangle A, C be equal to the square on B; I say that, as A is to B, so is B to C.
For, with the same construction, since the rectangle A, C is equal to the square on B, while the square on B is the rectangle B, D, for B is equal to D, therefore the rectangle A, C is equal to the rectangle B, D.
But, if the rectangle contained by the extremes be equal to that contained by the means, the four straight lines are proportional. [VI. 16]
Therefore, as A is to B, so is D to C.
But B is equal to D; therefore, as A is to B, so is B to C.
Therefore etc. Q. E. D.
