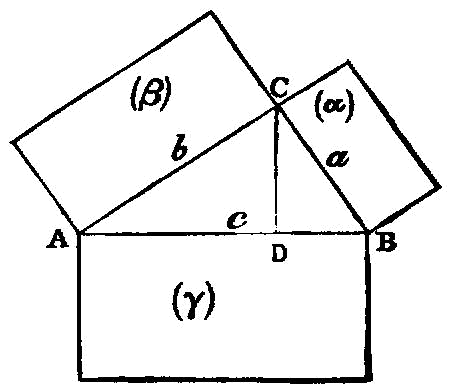
In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.

Let ABC be a right-angled triangle having the angle BAC right; I say that the figure on BC is equal to the similar and similarly described figures on BA, AC.

Let AD be drawn perpendicular.

Then since, in the right-angled triangle ABC, AD has been drawn from the right angle at A perpendicular to the base BC, the triangles ABD, ADC adjoining the perpendicular are similar both to the whole ABC and to one another. [VI. 8]

And, since ABC is similar to ABD, therefore, as CB is to BA, so is AB to BD. [VI. Def. 1]

And, since three straight lines are proportional, as the first is to the third, so is the figure on the first to the similar and similarly described figure on the second. [VI. 19, Por.]

Therefore, as CB is to BD, so is the figure on CB to the similar and similarly described figure on BA.

For the same reason also, as BC is to CD, so is the figure on BC to that on CA; so that, in addition, as BC is to BD, DC, so is the figure on BC to the similar and similarly described figures on BA, AC.

But BC is equal to BD, DC; therefore the figure on BC is also equal to the similar and similarly described figures on BA, AC.

Therefore etc. Q. E. D.