Proposition I.37
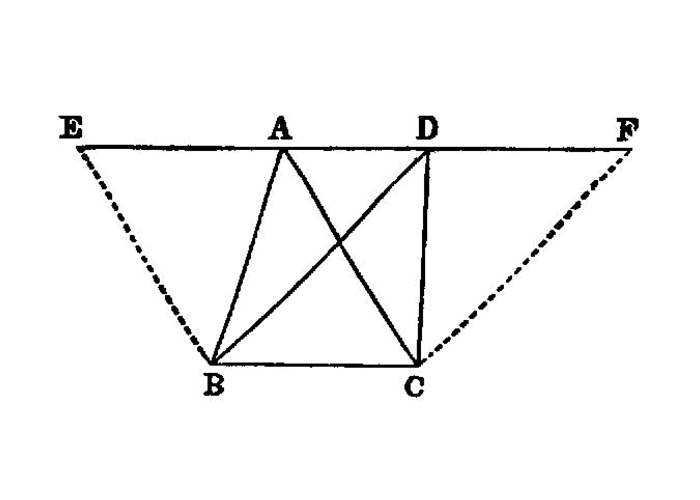
Triangles which are on the same base and in the same parallels are equal to one another.
Let ABC, DBC be triangles on the same base BC and in the same parallels AD, BC; I say that the triangle ABC is equal to the triangle DBC.
Let AD be produced in both directions to E, F; through B let BE be drawn parallel to CA, I.31 and through C let CF be drawn parallel to BD. I.31
Then each of the figures EBCA, DBCF is a parallelogram; and they are equal,
for they are on the same base BC and in the same parallels BC, EF. I.35
Moreover the triangle ABC is half of the parallelogram EBCA; for the diameter AB bisects it. I.34
And the triangle DBC is half of the parallelogram DBCF; for the diameter DC bisects it. I.34
[But the halves of equal things are equal to one another.] 1
Therefore the triangle ABC is equal to the triangle DBC.
Therefore etc.
- Q. E. D.
References
Footnotes
-
But the halves of equal things are equal to one another
Here and in the next proposition Heiberg brackets the wordsBut the halves of equal things are equal to one another
on the ground that, since theCommon Notion which asserted this fact was interpolated at a very early date (before the time of Theon), it is probable that the words here were interpolated at the same time. Cf. note above (p. 224) on the interpolatedCommon Notion . ↩
