Proposition I.16

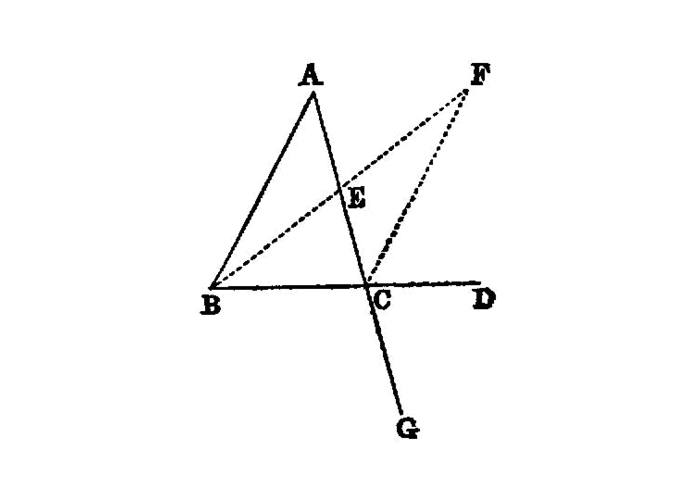
In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles.

Let ABC be a triangle, and let one side of it BC be produced to D;

I say that the exterior angle 1 ACDis greater than either of the interior and opposite angles 2 CBA, BAC.

Let AC be bisected at E I.10, and let BE be joined and produced in a straight line to F;

let EF be made equal to BEI.3, let FC be joined I.post.1, and let AC be drawn through to G 3 I.post.2.

Then, since AE is equal to EC, and BE to EF,

  • the two sides AE, EB are equal to the two sides CE, EF respectively; and the angle AEB is equal to the angle FEC, for they are vertical angles. I.15 Therefore the base AB is equal to the base FC, and the triangle ABE is equal to the triangle CFE 4, and the remaining angles are equal to the remaining angles respectively, namely those which the equal sides subtend; I.4 therefore the angle BAE is equal to the angle ECF.

But the angle ECD is greater than the angle ECF; I.c.n.5

  • therefore the angle ACD is greater than the angle BAE.

Similarly also, if BC be bisected, the angle BCG, that is, the angle ACD I.15, can be proved greater than the angle ABC as well.

Therefore etc.

  • Q. E. D.

References

Footnotes

  1. the exterior angle,
    literally the outside angle, ἡ ἐκτὸς γωνία. ↩

  2. the interior and opposite angles,

    τῶν ἐντὸς καὶ ἀπεναντίον γωνιῶν

    ↩

  3. let AC be drawn through to G.
    The word is διήχθω, a variation on the more usual ἐκβεβλήσθω, let it be produced. ↩

  4. CFE,
    in the text FEC. ↩