Proposition I.21
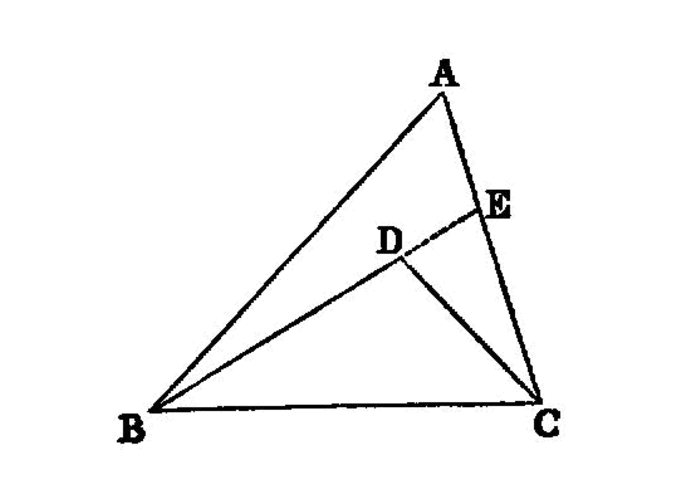
If on one of the sides of a triangle, from its extremities, there be constructed two straight lines meeting within the triangle,1 the straight lines so constructed 2 will be less than the remaining two sides of the triangle, but will contain a greater angle.
On BC, one of the sides of the triangle ABC, from its extremities B, C, let the two straight lines BD, DC be constructed meeting within the triangle;
I say that BD, DC are less than the remaining two sides of the triangle BA, AC, but contain an angle BDC greater than the angle BAC.
For let BD be drawn through to E.
Then, since in any triangle two sides are greater than the remaining one, I.20
- therefore, in the triangle
ABE, the two sidesAB,AEare greater thanBE.
Let EC be added to each;
- therefore
BA,ACare greater thanBE,EC.
Again, since, in the triangle CED,
- the two sides
CE,EDare greater thanCD, letDBbe added to each; thereforeCE,EBare greater thanCD,DB.
But BA, AC were proved greater than BE, EC;
- therefore
BA,ACare much greater thanBD,DC.
Again, since in any triangle the exterior angle is greater than the interior and opposite angle, I.16 therefore, in the triangle CDE,
- the exterior angle
BDCis greater than the angleCED.
For the same reason, moreover, in the triangle ABE also,
- the exterior angle
CEBis greater than the angleBAC.
But the angle BDC was proved greater than the angle CEB;
- therefore the angle
BDCis much greater than the angleBAC.
Therefore etc.
- Q. E. D.
References
Footnotes
-
be constructed...meeting within the triangle.
The wordmeeting
is not in the Greek, where the words areἐντὸς συσταθῶσιν. συνίστασθαι is the word used of constructing two straight lines to a point (cf. I. 7) or so as to form a triangle; but it is necessary in English to indicate that they meet. ↩ -
the straight lines so constructed.
Observe the elegant brevity of the Greekαἱ συσταθεῖσαι . ↩
