Proposition I.24
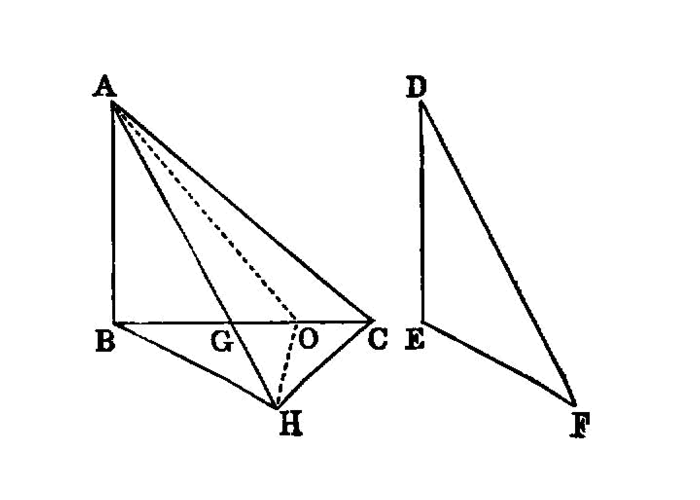
If two triangles have the two sides equal to two sides respectively, but have the one of the angles contained by the equal straight lines greater than the other, they will also have the base greater than the base.
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE, and AC to DF, and let the angle at A be greater than the angle at D;
I say that the base BC is also greater than the base EF. 1
For, since the angle BAC is greater than the angle EDF, let there be constructed, on the straight line DE, and at the point D on it, the angle EDG equal to the angle BAC; I.23 let DG be made equal to either of the two straight lines AC, DF, and let EG, FG be joined.
Then, since AB is equal to DE, and AC to DG, the two sides BA, AC are equal to the two sides ED, DG, respectively;
- and the angle
BACis equal to the angleEDG; therefore the baseBCis equal to the baseEG. I.4
Again, since DF is equal to DG,
- the angle
DGFis also equal to the angleDFG; I.5 therefore the angleDFGis greater than the angleEGF.
Therefore the angle EFG is much greater than the angle EGF.
And, since EFG is a triangle having the angle EFG greater than the angle EGF,
- and the greater angle is subtended by the greater side, I.19 the side
EGis also greater thanEF.
But EG is equal to BC.
- Therefore
BCis also greater thanEF.
Therefore etc.
- Q. E. D.
References
Footnotes
-
I say that the base
BCis also greater than the baseEF.
I have naturally left out the well-known words added by Simson in order to avoid the necessity of considering three cases:Of the two sides
DE,DFletDEbe the side which is not greater than the other.
I doubt whether Euclid could have been induced to insert the words himself, even if it had been represented to him that their omission meant leaving two possible cases out of consideration. His habit and that of the great Greek geometers was, not to set out all possible cases, but to give as a rule one case, generally the most difficult, as here, and to leave the others to the reader to work out for himself. We have already seen one instance in I. 7. ↩
