Proposition I.27
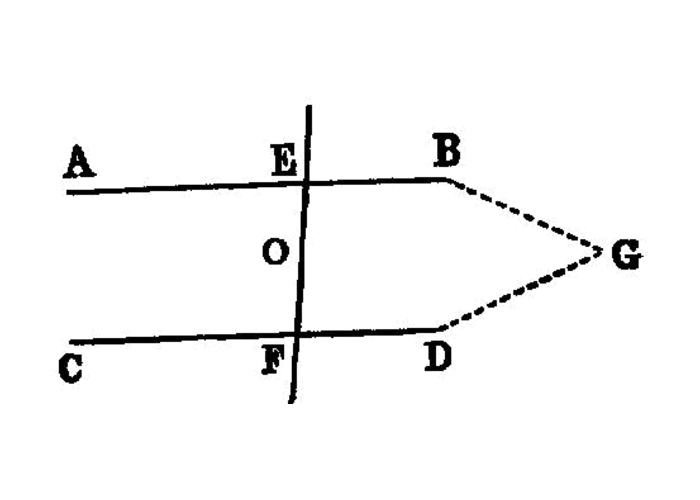
If a straight line falling on two straight lines 1 make the alternate angles [^I.27:2] equal to one another, the straight lines will be parallel to one another.
For let the straight line EF falling on the two straight lines AB, CD make the alternate angles AEF, EFD equal to one another;
I say that AB is parallel to CD.
For, if not, AB, CD when produced will meet either in the direction of B, D or towards A, C. [^I.27:3]
Let them be produced and meet, in the direction of B, D, at G.
Then, in the triangle GEF, the exterior angle AEF is equal to the interior and opposite angle EFG: which is impossible. I.16
Therefore AB, CD when produced will not meet in the direction of B, D.
Similarly it can be proved that neither will they meet towards A, C.
But straight lines which do not meet in either direction are parallel; I.def.23
- therefore
ABis parallel toCD.
Therefore etc.
- Q. E. D.
References
Footnotes
[^I.27:2] the alternate angles,
-
falling on two straight lines,
εὶς δύο εὐθείας ἐμπίπτουσα
