Proposition I.28
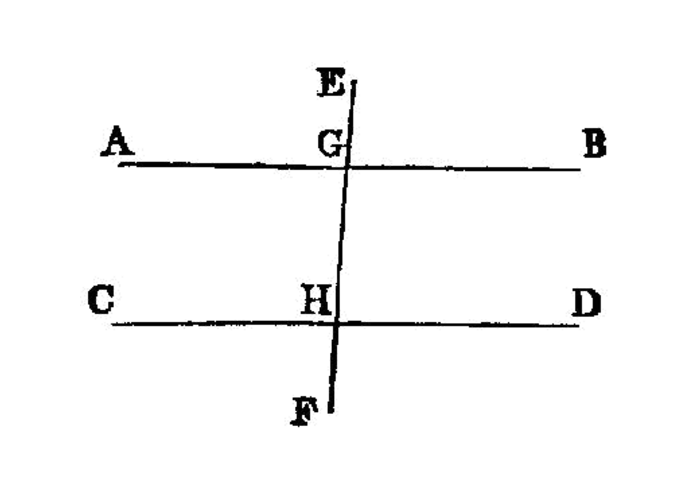
If a straight line falling on two straight lines make the exterior angle equal to the interior and opposite angle on the same side, or the interior angles on the same side equal to two right angles, the straight lines will be parallel to one another.
For let the straight line EF falling on the two straight lines AB, CD make the exterior angle EGB equal to the interior and opposite angle GHD, or the interior angles on the same side, namely BGH, GHD, equal to two right angles;
I say that AB is parallel to CD.
For, since the angle EGB is equal to the angle GHD, while the angle EGB is equal to the angle AGH, I.15 the angle AGH is also equal to the angle GHD; and they are alternate;
- therefore
ABis parallel toCD. I.27
Again, since the angles BGH, GHD are equal to two right angles, and the angles AGH, BGH are also equal to two right angles, I.13 the angles AGH, BGH are equal to the angles BGH, GHD.
Let the angle BGH be subtracted from each; therefore the remaining angle AGH is equal to the remaining angle GHD; and they are alternate;
- therefore
ABis parallel toCD. I.27
Therefore etc.
- Q. E. D.
