Proposition I.42
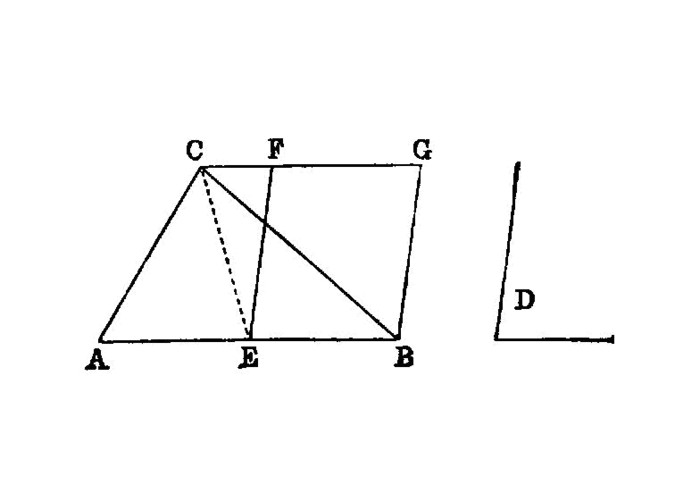
To construct, in a given rectilineal angle, a parallelogram equal to a given triangle.
Let ABC be the given triangle, and D the given rectilineal angle; thus it is required to construct in the rectilineal angle D a parallelogram equal to the triangle ABC.
Let BC be bisected at E, and let AE be joined; on the straight line EC, and at the point E on it, let the angle CEF be constructed equal to the angle D; I.23 through A let AG be drawn parallel to EC, and I.31 through C let CG be drawn parallel to EF.
Then FECG is a parallelogram.
And, since BE is equal to EC,
- the triangle
ABEis also equal to the triangleAEC, for they are on equal basesBE,ECand in the same parallelsBC,AG; I.38 therefore the triangleABCis double of the triangleAEC.
But the parallelogram FECG is also double of the triangle AEC, for it has the same base with it and is in the same parallels with it; I.41
- therefore the parallelogram
FECGis equal to the triangleABC.
And it has the angle CEF equal to the given angle D.
Therefore the parallelogram FECG has been constructed equal to the given triangle ABC, in the angle CEF which is equal to D.
- Q. E. F.
