Proposition I.47
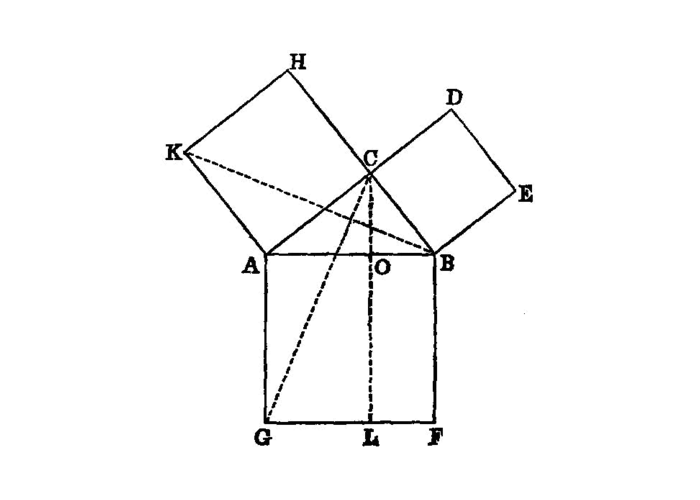
In right-angled triangles the square on 1 the side subtending the right angle 2 is equal to the squares on the sides containing the right angle.
Let ABC be a right-angled triangle having the angle BAC right;
I say that the square on BC is equal to the squares on BA, AC.
For let there be described on BC the square BDEC, and on BA, AC the squares GB, HC; I.46 through A let AL be drawn parallel to either BD or CE, and let AD, FC be joined.
Then, since each of the angles BAC, BAG is right, it follows that with a straight line BA, and at the point A on it, the two straight lines AC, AG not lying on the same side make the adjacent angles equal to two right angles;
- therefore
CAis in a straight line withAG. I.14
For the same reason
BAis also in a straight line withAH.
And, since the angle DBC is equal to the angle FBA: for each is right: let the angle ABC be added to each;
- therefore the whole angle
DBAis equal to the whole angleFBC. I.c.n.2
And, since DB is equal to BC, and FB to BA, the two sides AB, BD are equal to the two sides FB, BC respectively, 3
- and the angle
ABDis equal to the angleFBC; therefore the baseADis equal to the baseFC, and the triangleABDis equal to the triangleFBC. I.4
Now the parallelogram BL is double of the triangle ABD, for they have the same base BD and are in the same parallels BD, AL. I.41
And the square GB is double of the triangle FBC, for they again have the same base FB and are in the same parallels FB, GC. I.41
[But the doubles of equals are equal to one another.] 4
- Therefore the parallelogram
BLis also equal to the squareGB.
Similarly, if AE, BK be joined, the parallelogram CL can also be proved equal to the square HC;
- therefore the whole square
BDECis equal to the two squaresGB,HC. I.c.n.2
And the square BDEC is described on BC,
- and the squares
GB,HConBA,AC.
Therefore the square on the side BC is equal to the squares on the sides BA, AC.
Therefore etc.
- Q. E. D.
References
Footnotes
-
the square on
,τὸ ἀπὸ...τετρἁγωνον , the wordἀναγραφέν orἀναγεγραμμένον being understood. ↩ -
subtending the right angle.
Hereὑποτεινούσης ,subtending,
is used with the simple accusative (τὴν ὀρθὴν γωνίαν ) instead of being followed byὑπό and the accusative, which seems to be the original and more orthodox construction. Cf. I. 18, note. ↩ -
the two sides AB, BD....
Euclid actually writes
and therefore the equal sides in the two triangles are not mentioned in corresponding order, though he adheres to the wordsDB,BA,ἑκατέρα ἑκατέρα respectively.
HereDBis equal toBCandBAtoFB. ↩ -
[But the doubles of equals are equal to one another.]
Heiberg brackets these words as an interpolation, since it quotes aCommon Notion which is itself interpolated. Cf. note on I. 37, p. 332, and on interpolatedCommon Notions , pp. 223-4. ↩


