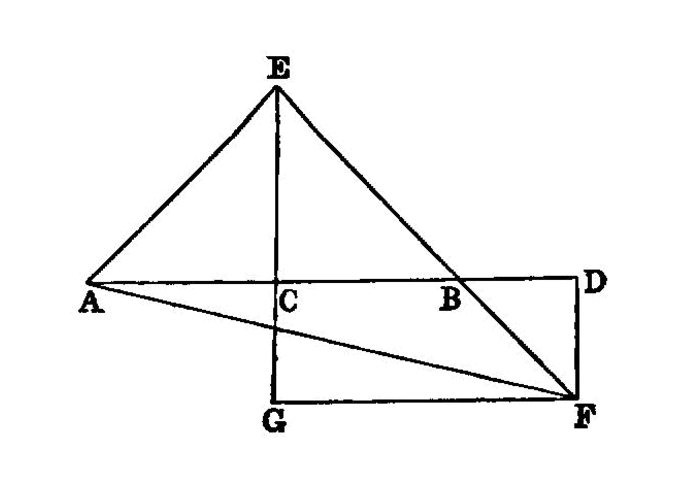
For let a straight line AB be bisected at C, and let a straight line BD be added to it in a straight line;

I say that the squares on AD, DB are double of the squares on AC, CD.

For let CE be drawn from the point C at right angles to AB [I. 11], and let it be made equal to either AC or CB [I. 3]; let EA, EB be joined; through E let EF be drawn parallel to AD, and through D let FD be drawn parallel to CE. [I. 31]

Then, since a straight line EF falls on the parallel straight lines EC, FD, the angles CEF, EFD are equal to two right angles; [I. 29] therefore the angles FEB, EFD are less than two right angles.

But straight lines produced from angles less than two right angles meet; [I. Post. 5] therefore EB, FD, if produced in the direction B, D, will meet.

Let them be produced and meet at G, and let AG be joined.

Then, since AC is equal to CE, the angle EAC is also equal to the angle AEC; [I. 5] and the angle at C is right; therefore each of the angles EAC, AEC is half a right angle. [I. 32]

For the same reason each of the angles CEB, EBC is also half a right angle; therefore the angle AEB is right.

And, since the angle EBC is half a right angle, the angle DBG is also half a right angle. [I. 15] But the angle BDG is also right, for it is equal to the angle DCE, they being alternate; [I. 29] therefore the remaining angle DGB is half a right angle; [I. 32] therefore the angle DGB is equal to the angle DBG, so that the side BD is also equal to the side GD. [I. 6]

Again, since the angle EGF is half a right angle, and the angle at F is right, for it is equal to the opposite angle, the angle at C, [I. 34] the remaining angle FEG is half a right angle; [I. 32] therefore the angle EGF is equal to the angle FEG, so that the side GF is also equal to the side EF. [I. 6]

Now, since the square on EC is equal to the square on CA, the squares on EC, CA are double of the square on CA.

But the square on EA is equal to the squares on EC, CA; [I. 47] therefore the square on EA is double of the square on AC. [C. N. 1]

Again, since FG is equal to EF, the square on FG is also equal to the square on FE; therefore the squares on GF, FE are double of the square on EF.

But the square on EG is equal to the squares on GF, FE; [I. 47] therefore the square on EG is double of the square on EF.

And EF is equal to CD; [I. 34] therefore the square on EG is double of the square on CD. But the square on EA was also proved double of the square on AC; therefore the squares on AE, EG are double of the squares on AC, CD.

And the square on AG is equal to the squares on AE, EG; [I. 47] therefore the square on AG is double of the squares on AC, CD. But the squares on AD, DG are equal to the square on AG; [I. 47] therefore the squares on AD, DG are double of the squares on AC, CD.

And DG is equal to DB; therefore the squares on AD, DB are double of the squares on AC, CD.

Therefore etc. Q. E. D.