Proposition 2.4

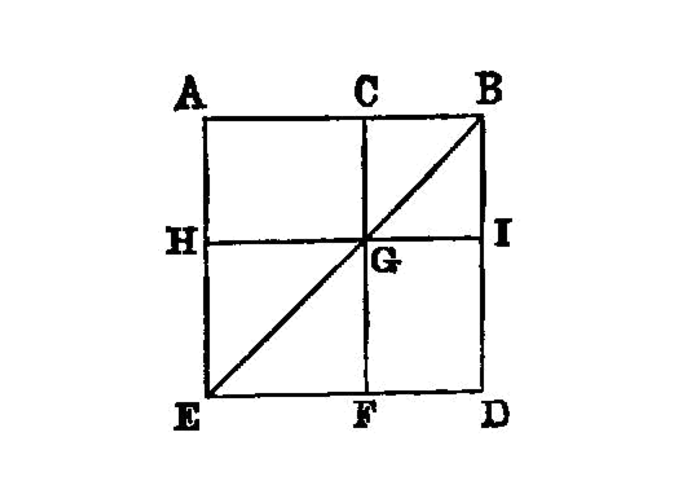
If a straight line be cut at random, the square on the whole is equal to the squares on the segments and twice the rectangle contained by the segments.

For let the straight line AB be cut at random at C; I say that the square on AB is equal to the squares on AC, CB and twice the rectangle contained by AC, CB.

For let the square ADEB be described on AB, [I. 46] let BD be joined; through C let CF be drawn parallel to either AD or EB, and through G let HK be drawn parallel to either AB or DE. [I. 31]

Then, since CF is parallel to AD, and BD has fallen on them, the exterior angle CGB is equal to the interior and opposite angle ADB. [I. 29]

But the angle ADB is equal to the angle ABD, since the side BA is also equal to AD; [I. 5] therefore the angle CGB is also equal to the angle GBC, so that the side BC is also equal to the side CG. [I. 6]

But CB is equal to GK, and CG to KB; [I. 34] therefore GK is also equal to KB; therefore CGKB is equilateral.

I say next that it is also right-angled.

For, since CG is parallel to BK, the angles KBC, GCB are equal to two right angles. [I. 29]

But the angle KBC is right; therefore the angle BCG is also right, so that the opposite angles CGK, GKB are also right. [I. 34]

Therefore CGKB is right-angled; and it was also proved equilateral; therefore it is a square; and it is described on CB.

For the same reason HF is also a square; and it is described on HG, that is AC. [I. 34]

Therefore the squares HF, KC are the squares on AC, CB.

Now, since AG is equal to GE, and AG is the rectangle AC, CB, for GC is equal to CB, therefore GE is also equal to the rectangle AC, CB.

Therefore AG, GE are equal to twice the rectangle AC, CB.

But the squares HF, CK are also the squares on AC, CB; therefore the four areas HF, CK, AG, GE are equal to the squares on AC, CB and twice the rectangle contained by AC, CB.

But HF, CK, AG, GE are the whole ADEB, which is the square on AB.

Therefore the square on AB is equal to the squares on AC, CB and twice the rectangle contained by AC, CB.

Therefore etc. Q. E. D.

twice the rectangle contained by the segments. By a curious idiom this is in Greek the rectangle twice contained by the segments. Similarly twice the rectangle contained by `AC`, `CB` is expressed as the rectangle twice contained by `AC`, `CB` (τὸ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχόμενον ὀρθογ<*>ώνιον).

described. 39, 45. the squares (before on ). These words are not in the Greek, which simply says that the squares are on (εἰσἱν ἀπό) their respective sides.

areas. It is necessary to supply some substantive (the Greek leaves it to be understood); and I prefer areas to figures.