Proposition 2.7
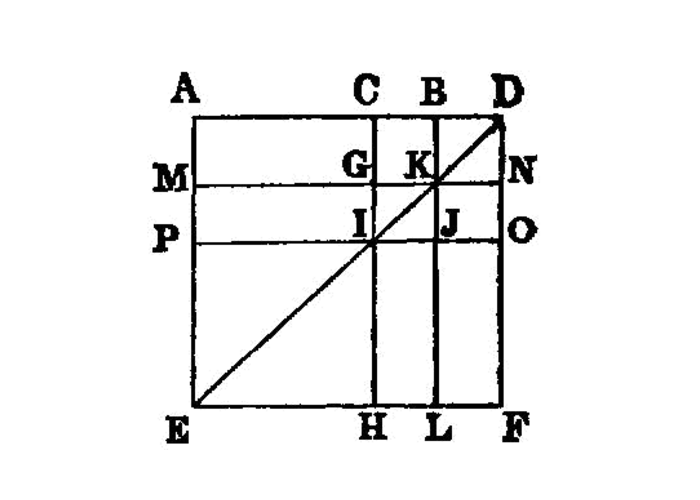
If a straight line be cut at random, the square on the whole and that on one of the segments both together are equal to twice the rectangle contained by the whole and the said segment and the square on the remaining segment.
For let a straight line AB be cut at random at the point C;
I say that the squares on AB, BC are equal to twice the rectangle contained by AB, BC and the square on CA.
For let the square ADEB be described on AB, [I. 46] and let the figure be drawn.
Then, since AG is equal to GE, [I. 43] let CF be added to each; therefore the whole AF is equal to the whole CE.
Therefore AF, CE are double of AF.
But AF, CE are the gnomon KLM and the square CF; therefore the gnomon KLM and the square CF are double of AF.
But twice the rectangle AB, BC is also double of AF; for BF is equal to BC; therefore the gnomon KLM and the square CF are equal to twice the rectangle AB, BC.
Let DG, which is the square on AC, be added to each; therefore the gnomon KLM and the squares BG, GD are equal to twice the rectangle contained by AB, BC and the square on AC.
But the gnomon KLM and the squares BG, GD are the whole ADEB and CF, which are squares described on AB, BC; therefore the squares on AB, BC are equal to twice the rectangle contained by AB, BC together with the square on AC.
Therefore etc. Q. E. D.
