Proposition 2.8
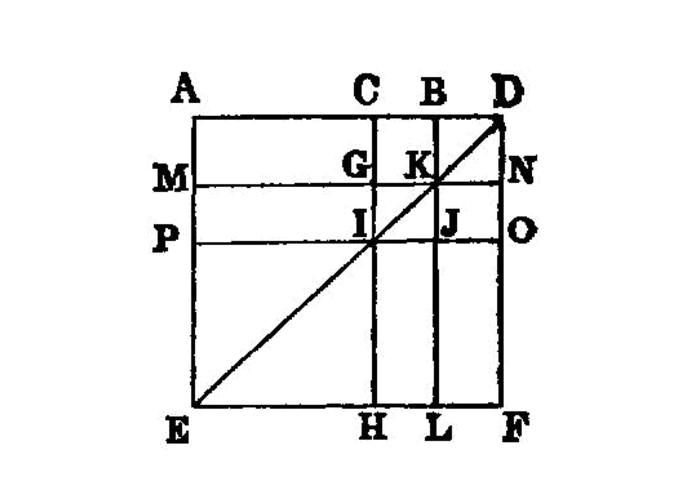
If a straight line be cut at random, four times the rectangle contained by the whole and one of the segments together with the square on the remaining segment is equal to the square described on the whole and the aforesaid segment as on one straight line.
For let a straight line AB be cut at random at the point C;
I say that four times the rectangle contained by AB, BC together with the square on AC is equal to the square described on AB, BC as on one straight line.
For let [the straight line] BD be produced in a straight line [with AB], and let BD be made equal to CB; let the square AEFD be described on AD, and let the figure be drawn double.
Then, since CB is equal to BD, while CB is equal to GK, and BD to KN, therefore GK is also equal to KN.
For the same reason QR is also equal to RP.
And, since BC is equal to BD, and GK to KN, therefore CK is also equal to KD, and GR to RN. [I. 36]
But CK is equal to RN, for they are complements of the parallelogram CP; [I. 43] therefore KD is also equal to GR; therefore the four areas DK, CK, GR, RN are equal to one another. Therefore the four are quadruple of CK.
Again, since CB is equal to BD, while BD is equal to BK, that is CG, and CB is equal to GK, that is GQ, therefore CG is also equal to GQ.
And, since CG is equal to GQ, and QR to RP, AG is also equal to MQ, and QL to RF. [I. 36]
But MQ is equal to QL, for they are complements of the parallelogram ML; [I. 43] therefore AG is also equal to RF; therefore the four areas AG, MQ, QL, RF are equal to one another. Therefore the four are quadruple of AG. But the four areas CK, KD, GR, RN were proved to be quadruple of CK; therefore the eight areas, which contain the gnomon STU, are quadruple of AK.
Now, since AK is the rectangle AB, BD, for BK is equal to BD, AB, BD is quadruple of AK.
But the gnomon STU was also proved to be quadruple of AK; therefore four times the rectangle AB, BD is equal to the gnomon STU.
Let OH, which is equal to the square on AC, be added to each; therefore four times the rectangle AB, BD together with the square on AC is equal to the gnomon STU and OH.
But the gnomon STU and OH are the whole square AEFD, which is described on AD. therefore four times the rectangle AB, BD together with the square on AC is equal to the square on AD
But BD is equal to BC; therefore four times the rectangle contained by AB, BC together with the square on AC is equal to the square on AD, that is to the square described on AB and BC as on one straight line.
Therefore etc. Q. E. D.
