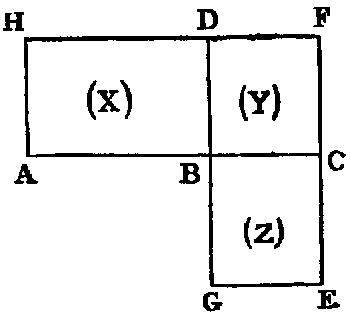
Equiangular parallelograms have to one another the ratio compounded of the ratios of their sides.

Let AC, CF be equiangular parallelograms having the angle BCD equal to the angle ECG; I say that the parallelogram AC has to the parallelogram CF the ratio compounded of the ratios of the sides.

For let them be placed so that BC is in a straight line with CG; therefore DC is also in a straight line with CE.

Let the parallelogram DG be completed; let a straight line K be set out, and let it be contrived that, as BC is to CG, so is K to L, and, as DC is to CE, so is L to M. [VI. 12]

Then the ratios of K to L and of L to M are the same as the ratios of the sides, namely of BC to CG and of DC to CE.

But the ratio of K to M is compounded of the ratio of K to L and of that of L to M; so that K has also to M the ratio compounded of the ratios of the sides.

Now since, as BC is to CG, so is the parallelogram AC to the parallelogram CH, [VI. 1] while, as BC is to CG, so is K to L, therefore also, as K is to L, so is AC to CH. [V. 11]

Again, since, as DC is to CE, so is the parallelogram CH to CF, [VI. 1] while, as DC is to CE, so is L to M, therefore also, as L is to M, so is the parallelogram CH to the parallelogram CF. [V. 11]

Since then it was proved that, as K is to L, so is the parallelogram AC to the parallelogram CH, and, as L is to M, so is the parallelogram CH to the parallelogram CF, therefore, ex aequali, as K is to M, so is AC to the parallelogram CF.

But K has to M the ratio compounded of the ratios of the sides; therefore AC also has to CF the ratio compounded of the ratios of the sides.

Therefore etc. Q. E. D.