Proposition 6.24
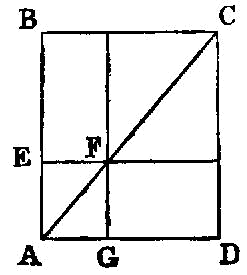
In any parallelogram the parallelograms about the diameter are similar both to the whole and to one another.
Let ABCD be a parallelogram, and AC its diameter, and let EG, HK be parallelograms about AC; I say that each of the parallelograms EG, HK is similar both to the whole ABCD and to the other.
For, since EF has been drawn parallel to BC, one of the sides of the triangle ABC, proportionally, as BE is to EA, so is CF to FA. [VI. 2]
Again, since FG has been drawn parallel to CD, one of the sides of the triangle ACD, proportionally, as CF is to FA, so is DG to GA. [VI. 2]
But it was proved that, as CF is to FA, so also is BE to EA; therefore also, as BE is to EA, so is DG to GA, and therefore, componendo, as BA is to AE, so is DA to AG, [V. 18] and, alternately, as BA is to AD, so is EA to AG. [V. 16]
Therefore in the parallelograms ABCD, EG, the sides about the common angle BAD are proportional.
And, since GF is parallel to DC,
For the same reason the triangle ACB is also equiangular with the triangle AFE, and the whole parallelogram ABCD is equiangular with the parallelogram EG.
Therefore, proportionally, as AD is to DC, so is AG to GF, as DC is to CA, so is GF to FA, as AC is to CB, so is AF to FE, and further, as CB is to BA, so is FE to EA.
And, since it was proved that, as DC is to CA, so is GF to FA, and, as AC is to CB, so is AF to FE, therefore,
Therefore in the parallelograms ABCD, EG the sides about the equal angles are proportional; therefore the parallelogram ABCD is similar to the parallelogram EG. [VI. Def. 1]
For the same reason the parallelogram ABCD is also similar to the parallelogram KH; therefore each of the parallelograms EG, HK is similar to ABCD.
But figures similar to the same rectilineal figure are also similar to one another; [VI. 21] therefore the parallelogram EG is also similar to the parallelogram HK.
Therefore etc. Q. E. D.
