Proposition I.12
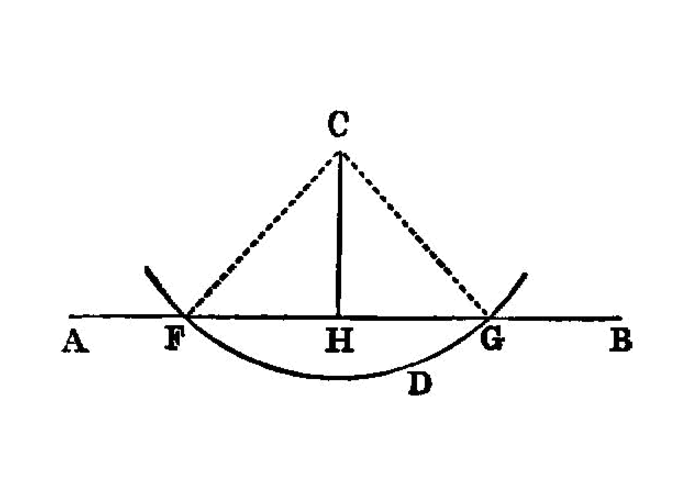
To a given infinite straight line, from a given point which is not on it, to draw a perpendicular straight line.1
Let AB be the given infinite straight line, and C the given point which is not on it; thus it is required to draw to the given infinite straight line AB, from the given point C which is not on it, a perpendicular straight line.
For let a point D be taken at random on the other side of the straight line AB2, and with centre C and distance CD let the circle EFG be described; I.post.3
- let the straight line
EGbe bisected atH, I.10 and let the straight linesCG,CH,CEbe joined. I.post.1
I say that CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.
For, since GH is equal to HE, and HC is common,
- the two sides
GH,HCare equal to the two sidesEH,HCrespectively;
and the base CG is equal to the base CE;
- therefore the angle
CHGis equal to the angleEHC. I.8 And they are adjacent angles.
But, when a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands. I.def.10
Therefore CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.
- Q. E. F.
References
Footnotes
-
a perpendicular straight line
,κάθετον εὐθεῖαν γραμμἡν . This is the full expression for a perpendicular,κάθετος meaning let fall or let down, so that the expression corresponds to our plumb-line.ἡ κάθετος is however constantly used alone for a perpendicular,γραμμἡ being understood. ↩ -
on the other side of the straight line AB
, literallytowards the other parts of the straight line
AB,ἐπὶ τὰ ἕτερα μέρη τῆς AB. Cf.on the same side
(ἐπὶ τὰ αὐτὰ μέρη ) in Post. 5 andin both directions
(ἐφ̓ ἑκάτερα τὰ μἑρη ) in Def. 23. ↩
