Proposition I.13
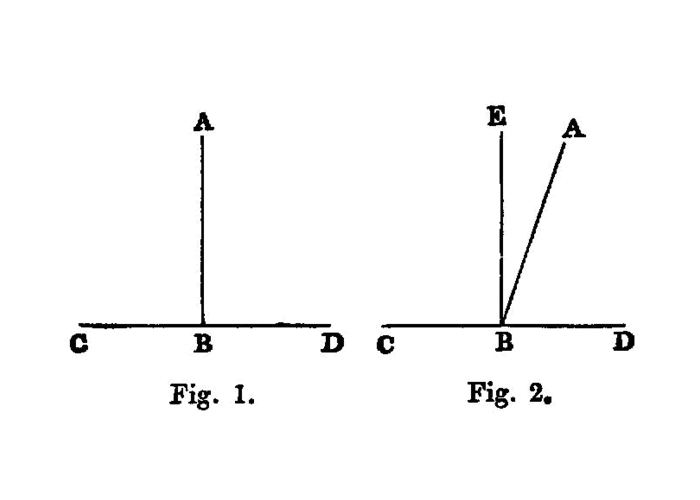
If a straight line set up on a straight line make angles, it will make either two right angles or angles equal to two right angles.
For let any straight line AB set up on the straight line CD make the angles CBA, ABD;
I say that the angles CBA, ABD are either two right angles or equal to two right angles.
Now, if the angle CBA is equal to the angle ABD,
- they are two right angles. [Def. 10]
But, if not, let BE be drawn from the point B at right angles to CD; [I. 11]
- therefore the angles
CBE,EBDare two right angles.
Then, since the angle CBE is equal to the two angles CBA, ABE,
- let the angle
EBDbe added to each; 1 therefore the anglesCBE,EBDare equal to the three anglesCBA,ABE,EBD. [C. N . 2]
Again, since the angle DBA is equal to the two angles DBE, EBA,
- let the angle
ABCbe added to each; therefore the anglesDBA.ABCare equal to the three anglesDBE,EBA,ABC. [C. N . 2]
But the angles CBE, EBD were also proved equal to the same three angles;
- and things which are equal to the same thing are also equal to one another; [
C. N . 1] therefore the anglesCBE,EBDare also equal to the anglesDBA,ABC.
But the angles CBE, EBD are two right angles;
- therefore the angles
DBA,ABCare also equal to two right angles.
Therefore etc.
- Q. E. D.
-
let the angle EBD be added to each,
literallylet the angle
EBDbe added (so as to be) common,κοινὴ προσκείσθω ἡ ὑπὸ ΕΒΔ . Similarlyκοινὴ ἀφηρήσθω is used of subtracting a straight line or angle from each of two others.Let the common angle
is clearly an inaccurate translation, for the angle is not common before it is added, i.e. theEBDbe addedκοινὴ is proleptic.Let the common angle be subtracted
as a translation ofκοινὴ ἀφηρήσθω would be less unsatisfactory, it is true, but, as it is desirable to use corresponding words when translating the two expressions, it seems hopeless to attempt to keep the wordcommon,
and I have therefore saidto each
andfrom each
simply. ↩
