Things which are equal to the same thing are also equal to one another.

Those magnitudes are said to be commensurable which are measured by the same measure, and those incommensurable which cannot have any common measure.

A solid is that which has length, breadth, and depth.

To draw a straight line from any point to any point.

Any rectangular parallelogram is said to be contained by the two straight lines containing the right angle.

Equal circles are those the diameters of which are equal, or the radii of which are equal.

Given a rational straight line and an apotome, if the square on the whole be greater than the square on the annex by the square on a straight line commensurable in length with the whole, and the whole be commensurable in length with the rational straight line set out, let the apotome be called a first apotome.

Given a rational straight line and a binomial, divided into its terms, such that the square on the greater term is greater than the square on the lesser by the square on a straight line commensurable in length with the greater, then, if the greater term be commensurable in length with the rational straight line set out, let the whole be called a first binomial straight line;

A magnitude is a part of a magnitude, the less of the greater, when it measures the greater.

A rectilineal figure is said to be inscribed in a rectilineal figure when the respective angles of the inscribed figure lie on the respective sides of that in which it is inscribed.

Similar rectilineal figures are such as have their angles severally equal and the sides about the equal angles proportional.

A point is that which has no part.

An unit is that by virtue of which each of the things that exist is called one.

Theory of angles, triangles, parallel lines, and parallelograms.

Triangles and parallelograms which are under the same height are to one another as their bases.

To find the centre of a given circle.

If a straight line be cut in extreme and mean ratio, the square on the greater segment added to the half of the whole is five times the square on the half.

If two similar plane numbers by multiplying one another make some number, the product will be square.

On a given finite straight line ¹ to construct an equilateral triangle.

If there be two straight lines, and one of them be cut into any number of segments whatever, the rectangle contained by the two straight lines is equal to the rectangles contained by the uncut straight line and each of the segments.

If there be as many numbers as we please in continued proportion, and the extremes of them be prime to one another, the numbers are the least of those which have the same ratio with them.

Into a given circle to fit a straight line equal to a given straight line which is not greater than the diameter of the circle.

Two unequal magnitudes being set out, if from the greater there be subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process be repeated continually, there will be left some magnitude which will be less than the lesser magnitude set out.

A part of a straight line cannot be in the plane of reference and a part in a plane more elevated.

Similar polygons inscribed in circles are to one another as the squares on the diameters.

To find the first binomial straight line.

To find the first apotome.

If there be any number of magnitudes whatever which are, respectively, equimultiples of any magnitudes equal in multitude, then, whatever multiple one of the magnitudes is of one, that multiple also will all be of all.

Two unequal numbers being set out, and the less being continually subtracted in turn from the greater, if the number which is left never measures the one before it until an unit is left, the original numbers will be prime to one another.

Similarly a figure is said to be circumscribed about a figure when the respective sides of the circumscribed figure pass through the respective angles of that about which it is circumscribed.

[Reciprocally related figures. See note.]

To produce a finite straight line continuously in a straight line.

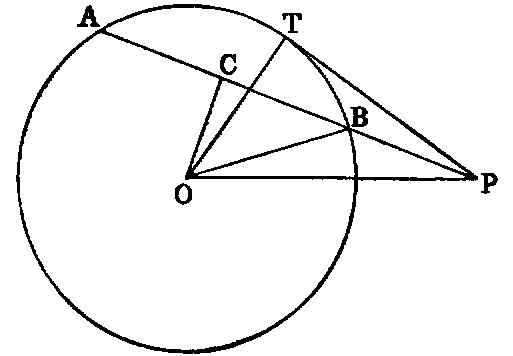
A straight line is said to touch a circle which, meeting the circle and being produced, does not cut the circle.

An extremity of a solid is a surface.

But if the annex be commensurable in length with the rational straight line set out, and the square on the whole be greater than that on the annex by the square on a straight line commensurable with the whole, let the apotome be called a second apotome.

but if the lesser term be commensurable in length with the rational straight line set out, let the whole be called a second binomial;

Straight lines are commensurable in square when the squares on them are measured by the same area, and incommensurable in square when the squares on them cannot possibly have any area as a common measure.

A line is breadthless length.

The greater is a multiple of the less when it is measured by the less.

And in any parallelogrammic area let any one whatever of the parallelograms about its diameter with the two complements be called a gnomon.

If equals be added to equals, the wholes are equal.

A number is a multitude composed of units.

Theory of Rectangles

• Regular postings on research and insights

Recast Euclid's Elements into a state-of-the-art framework

If two numbers by multiplying one another make a square number, they are similar plane numbers.

To place at a given point (as an extremity) a straight line equal to a given straight line.

Circles are to one another as the squares on the diameters.

If the square on a straight line be five times the square on a segment of it, then, when the double of the said segment is cut in extreme and mean ratio, the greater segment is the remaining part of the original straight line.

If on the circumference of a circle two points be taken at random, the straight line joining the points will fall within the circle.

To find numbers in continued proportion, as many as may be prescribed, and the least that are in a given ratio.

Given two numbers not prime to one another, to find their greatest common measure.

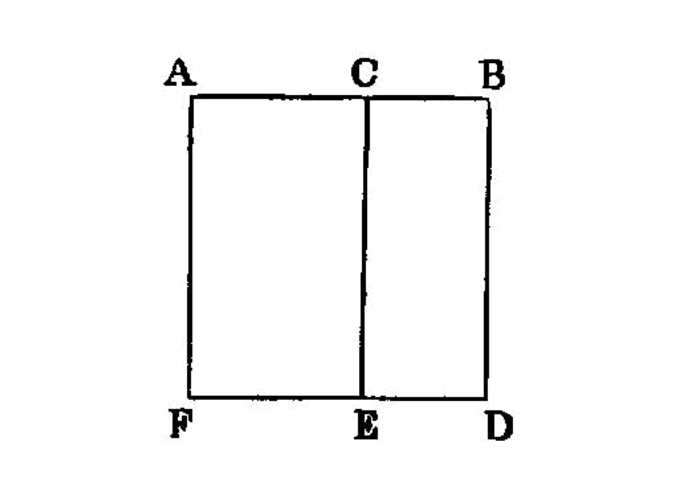
If a straight line be cut at random, the rectangle contained by the whole and both of the segments is equal to the square on the whole.

In a given circle to inscribe a triangle equiangular with a given triangle.

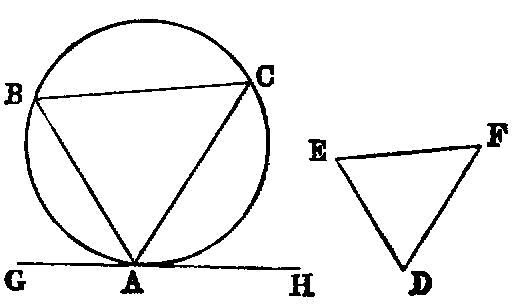
If, when the less of two unequal magnitudes is continually subtracted in turn from the greater, that which is left never measures the one before it, the magnitudes will be incommensurable.

If a first magnitude be the same multiple of a second that a third is of a fourth, and a fifth also be the same multiple of the second that a sixth is of the fourth, the sum of the first and fifth will also be the same multiple of the second that the sum of the third and sixth is of the fourth.

If a straight line be drawn parallel to one of the sides of a triangle, it will cut the sides of the triangle proportionally; and, if the sides of the triangle be cut proportionally, the line joining the points of section will be parallel to the remaining side of the triangle.

If two straight lines cut one another, they are in one plane, and every triangle is in one plane.

To find the second binomial straight line.

To find the second apotome.

A number is a part of a number, the less of the greater, when it measures the greater;

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.

But if neither be commensurable in length with the rational straight line set out, and the square on the whole be greater than the square on the annex by the square on a straight line commensurable with the whole, let the apotome be called a third apotome.

A rectilineal figure is said to be inscribed in a circle when each angle of the inscribed figure lies on the circumference of the circle.

A ratio is a sort of relation in respect of size between two magnitudes of the same kind.

With these hypotheses, it is proved that there exist straight lines infinite in multitude which are commensurable and incommensurable respectively, some in length only, and others in square also, with an assigned straight line. Let then the assigned straight line be called rational, and those straight lines which are commensurable with it, whether in length and in square or in square only, rational, but those which are incommensurable with it irrational.

The extremities of a line are points.

and if neither of the terms be commensurable in length with the rational straight line set out, let the whole be called a third binomial.

If equals be subtracted from equals, the remainders are equal.

A straight line is at right angles to a plane, when it makes right angles with all the straight lines which meet it and are in the plane.

To describe a circle with any centre and distance.

Theory of the Circle

Any pyramid which has a triangular base is divided into two pyramids equal and similar to one another, similar to the whole and having triangular bases, and into two equal prisms; and the two prisms are greater than the half of the whole pyramid.

Given two commensurable magnitudes, to find their greatest common measure.

If an angle of a triangle be bisected and the straight line cutting the angle cut the base also, the segments of the base will have the same ratio as the remaining sides of the triangle; and, if the segments of the base have the same ratio as the remaining sides of the triangle, the straight line joined from the vertex to the point of section will bisect the angle of the triangle.

If a cube number by multiplying itself make some number, the product will be cube.

If as many numbers as we please in continued proportion be the least of those which have the same ratio with them, the extremes of them are prime to one another.

If in a circle a straight line through the centre bisect a straight line not through the centre, it also cuts it at right angles; and if it cut it at right angles, it also bisects it.

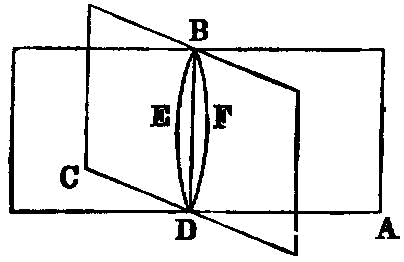
If two planes cut one another, their common section is a straight line.

Given two unequal straight lines, to cut off from the greater a straight line equal to the less.

If a straight line be cut in extreme and mean ratio, the square on the lesser segment added to the half of the greater segment is five times the square on the half of the greater segment.

Given three numbers not prime to one another, to find their greatest common measure.

If a first magnitude be the same multiple of a second that a third is of a fourth, and if equimultiples be taken of the first and third, then also ex aequali the magnitudes taken will be equimultiples respectively, the one of the second and the other of the fourth.

About a given circle to circumscribe a triangle equiangular with a given triangle.

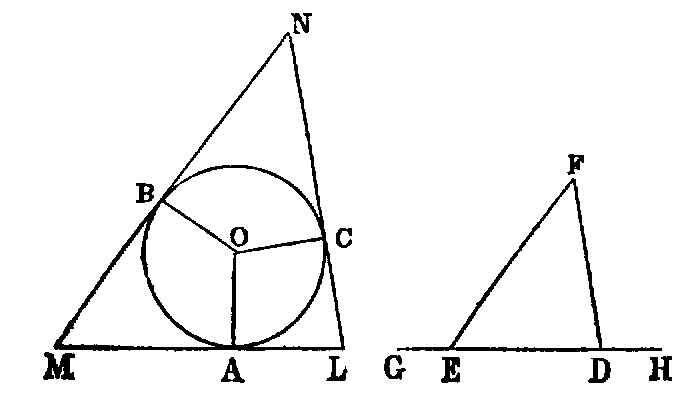
If a straight line be cut at random, the rectangle contained by the whole and one of the segments is equal to the rectangle contained by the segments and the square on the aforesaid segment.

To find the third binomial straight line.

To find the third apotome.

posting regular research and education videos

A plane is at right angles to a plane when the straight lines drawn, in one of the planes, at right angles to the common section of the planes are at right angles to the remaining plane.

And let the square on the assigned straight line be called rational and those areas which are commensurable with it rational, but those which are incommensurable with it irrational, and the straight lines which produce them irrational, that is, in case the areas are squares, the sides themselves, but in case they are any other rectilineal figures, the straight lines on which are described squares equal to them.

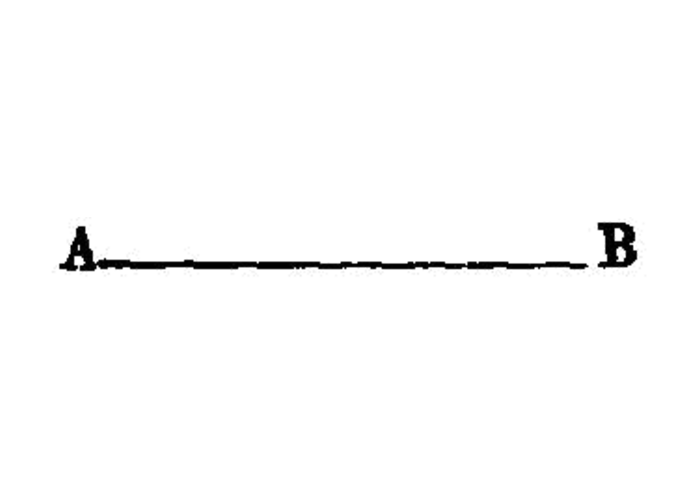
A straight line is a line which lies evenly with the points on itself.

A rectilineal figure is said to be circumscribed about a circle, when each side of the circumscribed figure touches the circumference of the circle.

Things which coincide with one another are equal to one another.

That all right angles are equal to one another.

The height of any figure is the perpendicular drawn from the vertex to the base.

Magnitudes are said to have a ratio to one another which are capable, when multiplied, of exceeding one another.

Again, if the square on the whole be greater than the square on the annex by the square on a straight line incommensurable with the whole, then, if the whole be commensurable in length with the rational straight line set out, let the apotome be called a fourth apotome;

In a circle straight lines are said to be equally distant from the centre when the perpendiculars drawn to them from the centre are equal.

Again, if the square on the greater term be greater than the square on the lesser by the square on a straight line incommensurable in length with the greater, then, if the greater term be commensurable in length with the rational straight line set out, let the whole be called a fourth binomial;

but parts when it does not measure it.

Inscription and circumscription of triangles and of regular polygons in and about circles

All the development code for GEOMETOR is here. As well as out content platform - PHOTON

Given three commensurable magnitudes, to find their greatest common measure.

If a straight line be cut in extreme and mean ratio, the square on the whole and the square on the lesser segment together are triple of the square on the greater segment.

In a given triangle to inscribe a circle.

If a straight line be set up at right angles to two straight lines which cut one another, at their common point of section, it will also be at right angles to the plane through them.

If a cube number by multiplying a cube number make some number, the product will be cube.

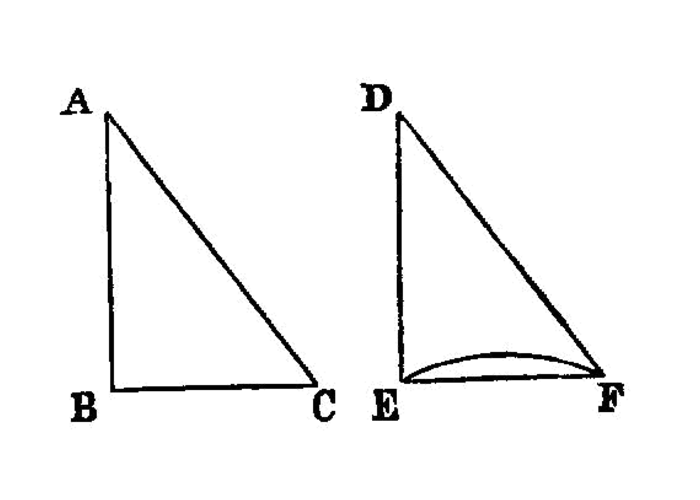
If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base ¹ equal to the base, the triangle will be equal to the triangle, and the remaining angles ² will be equal to the remaining angles respectively, ³ namely those which the equal sides subtend. ⁴

If in a circle two straight lines cut one another which are not through the centre, they do not bisect one another.

If there be two pyramids of the same height which have triangular bases, and cach of them be divided into two pyramids equal to one another and similar to the whole, and into two equal prisms, then, as the base of the one pyramid is to the base of the other pyramid, so will all the prisms in the one pyramid be to all the prisms, being equal in multitude, in the other pyramid.

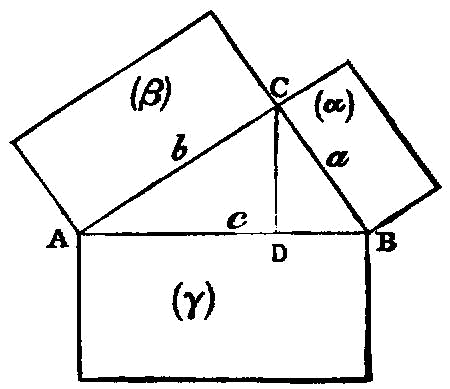
If a straight line be cut at random, the square on the whole is equal to the squares on the segments and twice the rectangle contained by the segments.

In equiangular triangles the sides about the equal angles are proportional, and those are corresponding sides which subtend the equal angles.

Given as many ratios as we please in least numbers, to find numbers in continued proportion which are the least in the given ratios.

Any number is either a part or parts of any number, the less of the greater.

If a first magnitude have to a second the same ratio as a third to a fourth, any equimultiples whatever of the first and third will also have the same ratio to any equimultiples whatever of the second and fourth respectively, taken in corresponding order.

To find the fourth binomial straight line.

To find the fourth apotome.

Similarly a circle is said to be inscribed in a figure when the circumference of the circle touches each side of the figure in which it is inscribed.

The whole is greater than the part.

The greater number is a multiple of the less when it is measured by the less.

That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

if the annex be so commensurable, a fifth;

if the lesser, a fifth binomial;

The inclination of a straight line to a plane is, assuming a perpendicular drawn from the extremity of the straight line which is elevated above the plane to the plane, and a straight line joined from the point thus arising to the extremity of the straight line which is in the plane, the angle contained by the straight line so drawn and the straight line standing up.

And that straight line is said to be at a greater distance on which the greater perpendicular falls.

A surface is that which has length and breadth only.

Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when, if any equimultiples whatever be taken of the first and third, and any equimultiples whatever of the second and fourth, the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively taken in corresponding order.

Theory of Proportion

This digital reference of Euclid's Elements is assembled from several English translations from over 100 years ago that are now in the public domain. The purpose of this project is to facilitate research and study of the dense information of the 13 books through intelligent navigation, robust taxonomies and comprehensive search.

If two circles cut one another, they will not have the same centre.

If a number be a part of a number, and another be the same part of another, the sum will also be the same part of the sum that the one is of the one.

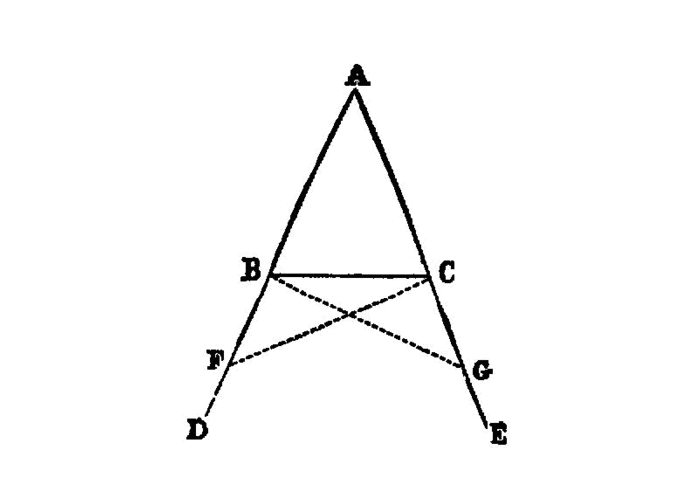
In isosceles triangles the angles at the base are equal to one another, and, if the equal straight ¹ lines be produced further, the angles under the base will be equal to one another.

Commensurable magnitudes have to one another the ratio which a number has to a number.

Plane numbers have to one another the ratio compounded of the ratios of their sides.

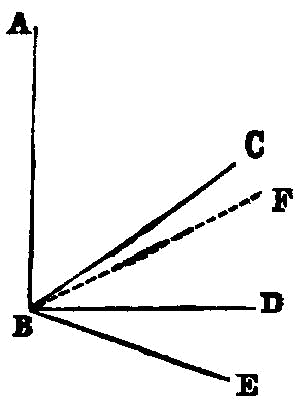
If a straight line be set up at right angles to three straight lines which meet one another, at their common point of section, the three straight lines are in one plane.

If a magnitude be the same multiple of a magnitude that a part subtracted is of a part subtracted, the remainder will also be the same multiple of the remainder that the whole is of the whole.

If a straight line be cut in extreme and mean ratio, and there be added to it a straight line equal to the greater segment, the whole straight line has been cut in extreme and mean ratio, and the original straight line is the greater segment.

About a given triangle to circumscribe a circle.

If two triangles have their sides proportional, the triangles will be equiangular and will have those angles equal which the corresponding sides subtend.

Pyramids which are of the same height and have triangular bases are to one another as the bases.

If a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half.

If a cube number by multiplying any number make a cube number, the multiplied number will also be cube.

To find the fifth binomial straight line.

To find the fifth apotome.

and, if neither, a sixth.

Let magnitudes which have the same ratio be called proportional.

The extremities of a surface are lines.

A segment of a circle is the figure contained by a straight line and a circumference of a circle.

and if neither, a sixth binomial.

The inclination of a plane to a plane is the acute angle contained by the straight lines drawn at right angles to the common section at the same point, one in each of the planes.

An even number is that which is divisible into two equal parts.

A circle is said to be circumscribed about a figure when the circumference of the circle passes through each angle of the figure about which it is circumscribed.

Application of the theory of proportion

To find the sixth binomial straight line.

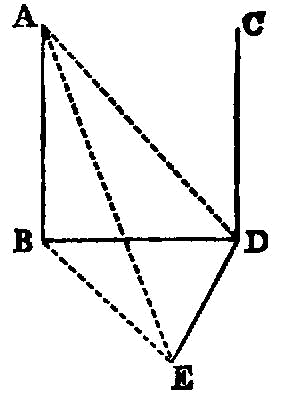
If two straight lines be at right angles to the same plane, the straight lines will be parallel.

In a given circle to inscribe a square.

If two triangles have one angle equal to one angle and the sides about the equal angles proportional, the triangles will be equiangular and will have those angles equal which the corresponding sides subtend.

If two magnitudes have to one another the ratio which a number has to a number, the magnitudes will be commensurable.

If a straight line be bisected and a straight line be added to it in a straight line, the rectangle contained by the whole with the added straight line and the added straight line together with the square on the half is equal to the square on the straight line made up of the half and the added straight line.

Pyramids which are of the same height and have polygonal bases are to one another as the bases.

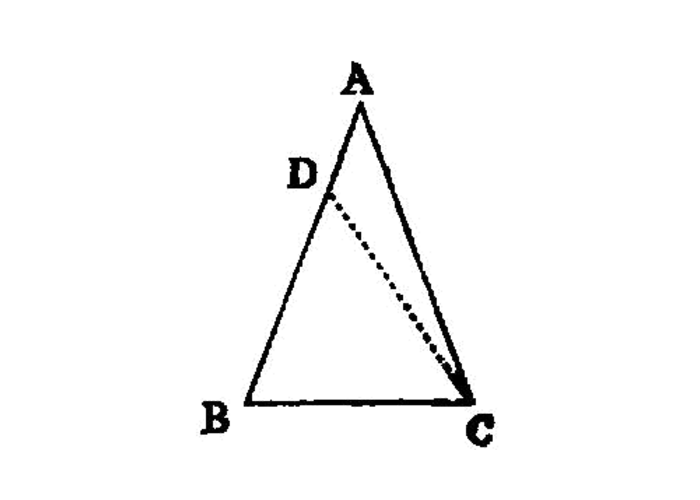
If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another.

If two magnitudes be equimultiples of two magnitudes, and any magnitudes subtracted from them be equimultiples of the same, the remainders also are either equal to the same or equimultiples of them.

If a number by multiplying itself make a cube number, it will itself also be cube.

If two circles touch one another, they will not have the same centre.

If a number be parts of a number, and another be the same parts of another, the sum will also be the same parts of the sum that the one is of the one.

If there be as many numbers as we please in continued proportion, and the first do not measure the second, neither will any other measure any other.

To find the sixth apotome.

An angle of a segment is that contained by a straight line and a circumference of a circle.

A plane is said to be similarly inclined to a plane as another is to another when the said angles of the inclinations are equal to one another.

When, of the equimultiples, the multiple of the first magnitude exceeds the multiple of the second, but the multiple of the third does not exceed the multiple of the fourth, then the first is said to have a greater ratio to the second than the third has to the fourth.

A straight line is said to be fitted into a circle when its extremities are on the circumference of the circle.

A plane surface is a surface which lies evenly with the straight lines on itself.

An odd number is that which is not divisible into two equal parts, or that which differs by an unit from an even number.

If an area be contained by a rational straight line and the first binomial, the side of the area is the irrational straight line which is called binomial.

If two triangles have one angle equal to one angle, the sides about other angles proportional, and the remaining angles either both less or both not less than a right angle, the triangles will be equiangular and will have those angles equal, the sides about which are proportional.

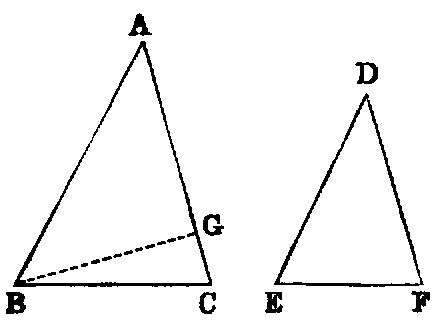
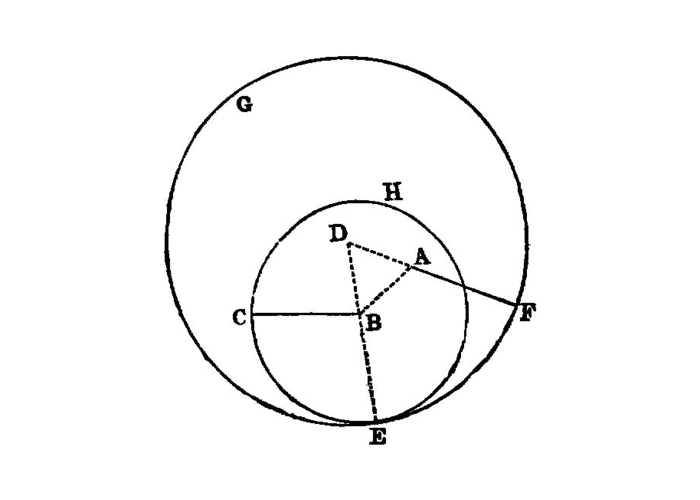
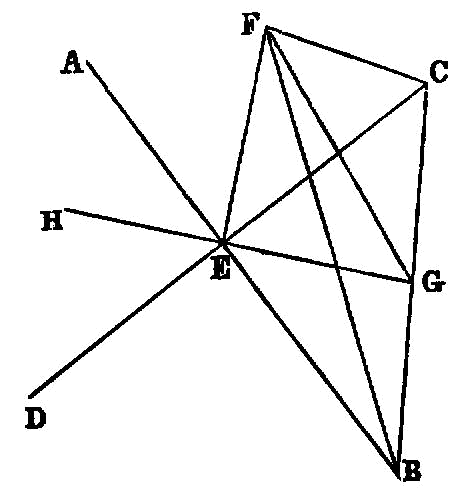
Given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there cannot be constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same extremity with it.

If there be as many numbers as we please in continued proportion, and the first measure the last, it will measure the second also.

Any prism which has a triangular base is divided into three pyramids equal to one another which have triangular bases.

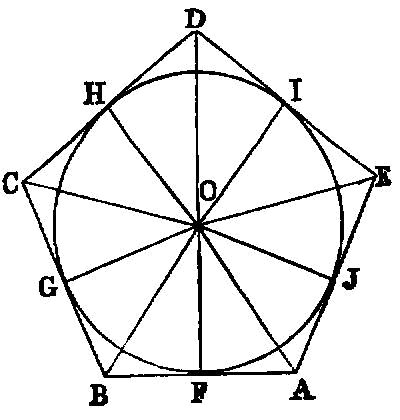
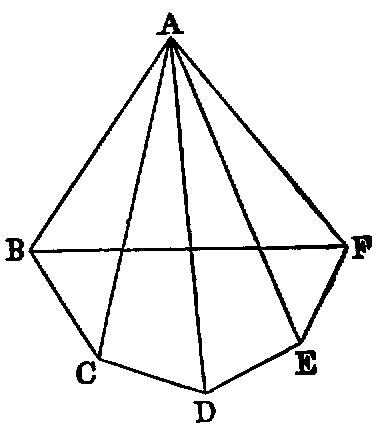
If three angles of an equilateral pentagon, taken either in order or not in order, be equal, the pentagon will be equiangular.

Incommensurable magnitudes have not to one another the ratio which a number has to a number.

If a straight line be cut at random, the square on the whole and that on one of the segments both together are equal to twice the rectangle contained by the whole and the said segment and the square on the remaining segment.

Equal magnitudes have to the same the same ratio, as also has the same to equal magnitudes.

If two straight lines be parallel and points be taken at random on each of them, the straight line joining the points is in the same plane with the parallel straight lines.

If a number be that part of a number, which a number subtracted is of a number subtracted, the remainder will also be the same part of the remainder that the whole is of the whole.

About a given circle to circumscribe a square.

If on the diameter of a circle a point be taken which is not the centre of the circle, and from the point straight lines fall upon the circle, that will be greatest on which the centre is, the remainder of the same diameter will be least, and of the rest the nearer to the straight line through the centre is always greater than the more remote, and only two equal straight lines will fall from the point on the circle, one on each side of the least straight line.

If a composite number by multiplying any number make some number, the product will be solid.

If an area be contained by a rational straight line and a first apotome, the side of the area is an apotome.

An even-times even number is that which is measured by an even number according to an even number.

An angle in a segment is the angle which, when a point is taken on the circumference of the segment and straight lines are joined from it to the extremities of the straight line which is the base of the segment, is contained by the straight lines so joined.

Parallel planes are those which do not meet.

A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.

A proportion in three terms is the least possible.

If an area be contained by a rational straight line and the second binomial, the side of the area is the irrational straight line which is called a first bimedial.

If in an equilateral and equiangular pentagon straight lines subtend two angles taken in order, they cut one another in extreme and mean ratio, and their greater segments are equal to the side of the pentagon.

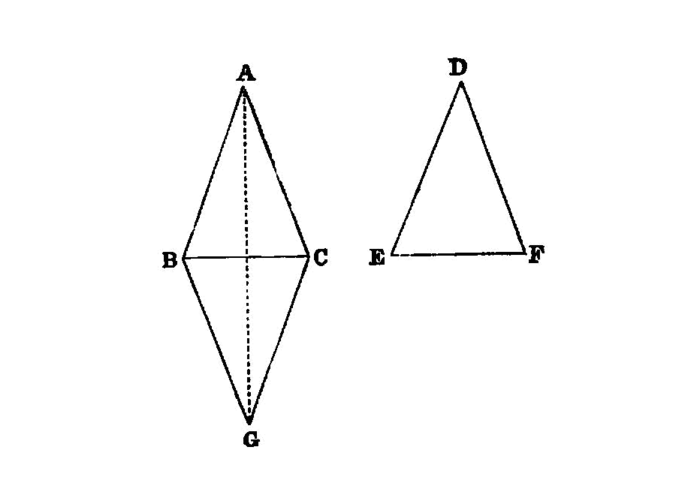
If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines.

In a given square to inscribe a circle.

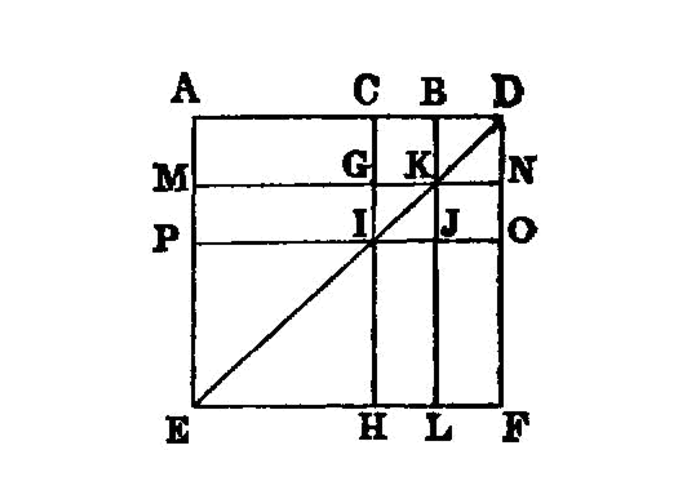
If a straight line be cut at random, four times the rectangle contained by the whole and one of the segments together with the square on the remaining segment is equal to the square described on the whole and the aforesaid segment as on one straight line.

If a number be the same parts of a number that a number subtracted is of a number subtracted, the remainder will also be the same parts of the remainder that the whole is of the whole.

If as many numbers as we please beginning from an unit be in continued proportion, the third from the unit will be square, as will also those which successively leave out one; the fourth will be cube, as will also all those which leave out two; and the seventh will be at once cube and square, as will also those which leave out five.

If two magnitudes have not to one another the ratio which a number has to a number, the magnitudes will be incommensurable.

Of unequal magnitudes, the greater has to the same a greater ratio than the less has; and the same has to the less a greater ratio than it has to the greater.

If between two numbers there fall numbers in continued proportion with them, then, however many numbers fall between them in continued proportion, so many will also fall in continued proportion between the numbers which have the same ratio with the original numbers.

If two straight lines be parallel, and one of them be at right angles to any plane, the remaining one will also be at right angles to the same plane.

Similar pyramids which have triangular bases are in the triplicate ratio of their corresponding sides.

If a point be taken outside a circle and from the point straight lines be drawn through to the circle, one of which is through the centre and the others are drawn at random, then, of the straight lines which fall on the concave circumference, that through the centre is greatest, while of the rest the nearer to that through the centre is always greater than the more remote, but, of the straight lines falling on the convex circumference, that between the point and the diameter is least, while of the rest the nearer to the least is always less than the more remote, and only two equal straight lines will fall on the circle from the point, one on each side of the least.

If in a right-angled triangle a perpendicular be drawn from the right angle to the base, the triangles adjoining the perpendicular are similar both to the whole and to one another.

If an area be contained by a rational straight line and a second apotome, the side of the area is a first apotome of a medial straight line.

assembly of research related to the project

And, when the straight lines containing the angle cut off a circumference, the angle is said to stand upon that circumference.

Similar solid figures are those contained by similar planes equal in multitude.

An even-times odd number is that which is measured by an even number according to an odd number.

And when the lines containing the angle are straight, the angle is called rectilineal.

When three magnitudes are proportional, the first is said to have to the third the duplicate ratio of that which it has to the second.

get and stay connected with phi ARCHITECT

If an area be contained by a rational straight line and the third binomial, the side of the area is the irrational straight line called a second bimedial.

The squares on straight lines commensurable in length have to one another the ratio which a square number has to a square number; and squares which have to one another the ratio which a square number has to a square number will also have their sides commensurable in length.

If the side of the hexagon and that of the decagon inscribed in the same circle be added together, the whole straight line has been cut in extreme and mean ratio, and its greater segment is the side of the hexagon.

If two numbers be prime to one another, and numbers fall between them in continued proportion, then, however many numbers fall between them in continued proportion, so many will also fall between each of them and an unit in continued proportion.

If as many numbers as we please beginning from an unit be in continued proportion, and the number after the unit be square, all the rest will also be square. And, if the number after the unit be cube, all the rest will also be cube.

About a given square to circumscribe a circle.

Magnitudes which have the same ratio to the same are equal to one another; and magnitudes to which the same has the same ratio are equal.

If a straight line be cut into equal and unequal segments, the squares on the unequal segments of the whole are double of the square on the half and of the square on the straight line between the points of section.

In equal pyramids which have triangular bases the bases are reciprocally proportional to the heights; and those pyramids in which the bases are reciprocally proportional to the heights are equal.

If a point be taken within a circle, and more than two equal straight lines fall from the point on the circle, the point taken is the centre of the circle.

To bisect a given rectilineal angle.

If a number be a part of a number, and another be the same part of another, alternately also, whatever part or parts the first is of the third, the same part, or the same parts, will the second also be of the fourth.

From a given straight line to cut off a prescribed part.

Straight lines which are parallel to the same straight line and are not in the same plane with it are also parallel to one another.

If an area be contained by a rational straight line and a third apotome, the side of the area is a second apotome of a medial straight line.

An odd-times odd number is that which is measured by an odd number according to an odd number.

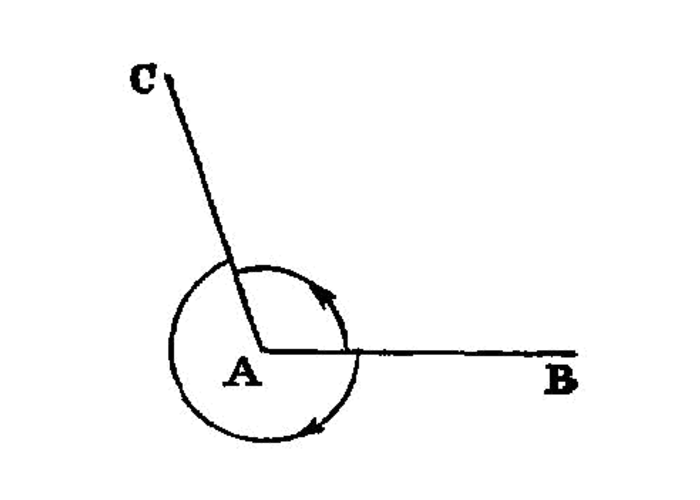
When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.

A sector of a circle is the figure which, when an angle is constructed at the centre of the circle, is contained by the straight lines containing the angle and the circumference cut off by them.

When four magnitudes are <continuously> proportional, the first is said to have to the fourth the triplicate ratio of that which it has to the second, and so on continually, whatever be the proportion.

Equal and similar solid figures are those contained by similar planes equal in multitude and in magnitude.

If numbers fall between each of two numbers and an unit in continued proportion, however many numbers fall between each of them and an unit in continued proportion, so many also will fall between the numbers themselves in continued proportion.

If as many numbers as we please beginning from an unit be in continued proportion, and the number after the unit be not square, neither will any other be square except the third from the unit and all those which leave out one. And, if the number after the unit be not cube, neither will any other be cube except the fourth from the unit and all those which leave out two.

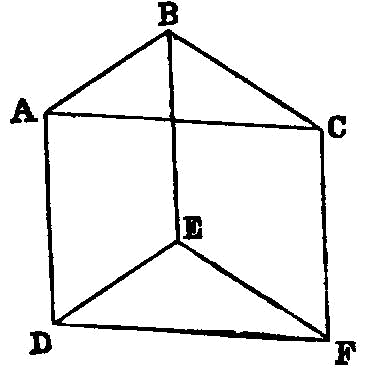
If two straight lines meeting one another be parallel to two straight lines meeting one another not in the same plane, they will contain equal angles.

Any cone is a third part of the cylinder which has the same base with it and equal height.

To find two straight lines incommensurable, the one in length only, and the other in square also, with an assigned straight line.

If a number be parts of a number, and another be the same parts of another, alternately also, whatever parts or part the first is of the third, the same parts or the same part will the second also be of the fourth.

If an equilateral pentagon be inscribed in a circle, the square on the side of the pentagon is equal to the squares on the side of the hexagon and on that of the decagon inscribed in the same circle.

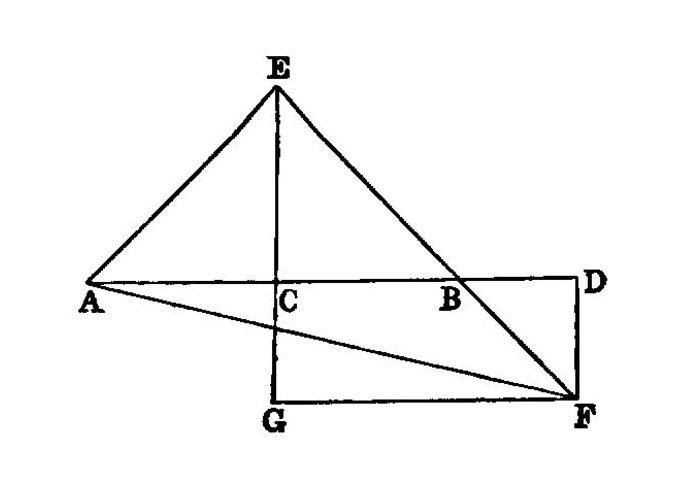
If a straight line be bisected, and a straight line be added to it in a straight line, the square on the whole with the added straight line and the square on the added straight line both together are double of the square on the half and of the square described on the straight line made up of the half and the added straight line as on one straight line.

Of magnitudes which have a ratio to the same, that which has a greater ratio is greater; and that to which the same has a greater ratio is less.

To cut a given uncut straight line similarly to a given cut straight line.

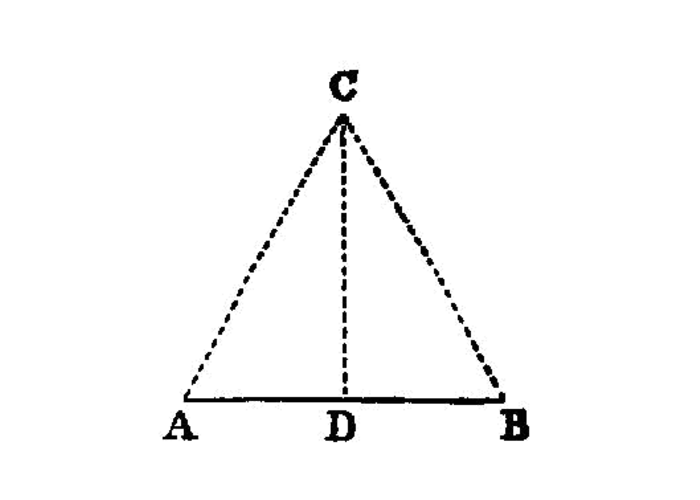
To bisect a given finite straight line.

To construct an isosceles triangle having each of the angles at the base double of the remaining one.

A circle does not cut a circle at more points than two.

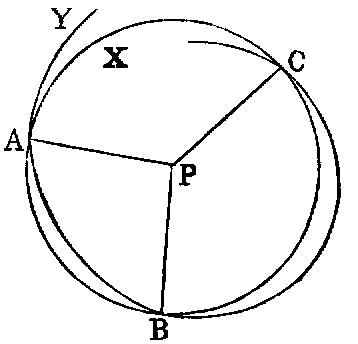
If an area be contained by a rational straight line and the fourth binomial, the side of the area is the irrational straight line called major.

If an area be contained by a rational straight line and a fourth apotome, the side of the area is minor.

The term corresponding magnitudes is used of antecedents in relation to antecedents, and of consequents in relation to consequents.

A prime number is that which is measured by an unit alone.

An obtuse angle is an angle greater than a right angle.

A solid angle is the inclination constituted by more than two lines which meet one another and are not in the same surface, towards all the lines.

Similar segments of circles are those which admit equal angles, or in which the angles are equal to one another.

Theory of planes, coplanar lines, and solid angles

Ratios which are the same with the same ratio are also the same with one another.

To two given straight lines to find a third proportional.

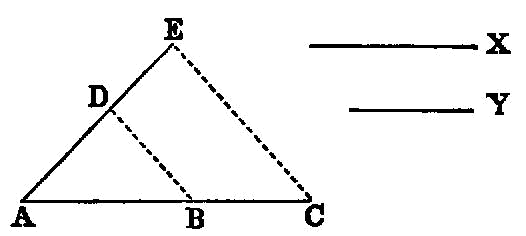
Between two square numbers there is one mean proportional number, and the square has to the square the ratio duplicate of that which the side has to the side.

Cones and cylinders which are of the same height are to one another as their bases.

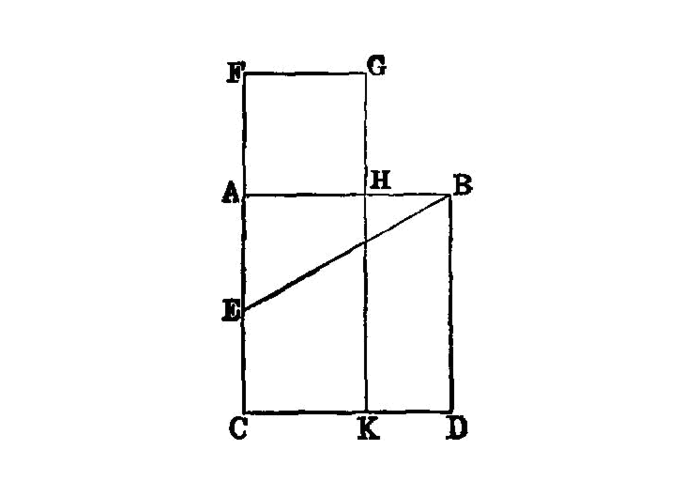
To cut a given straight line so that the rectangle contained by the whole and one of the segments is equal to the square on the remaining segment.

If two circles touch one another internally, and their centres be taken, the straight line joining their centres, if it be also produced, will fall on the point of contact of the circles.

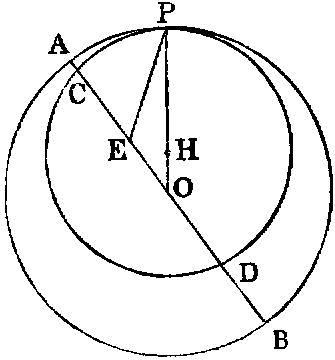
To draw a straight line at right angles to a given straight line from a given point on it.

In a given circle to inscribe an equilateral and equiangular pentagon.

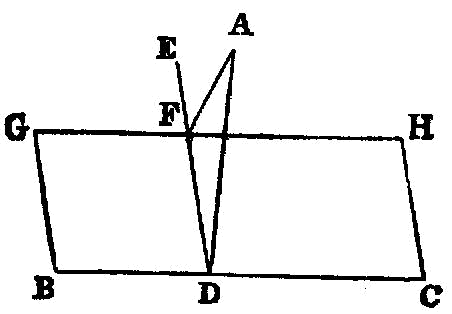
From a given elevated point to draw a straight line perpendicular to a given plane.

If four magnitudes be proportional, and the first be commensurable with the second, the third will also be commensurable with the fourth; and, if the first be incommensurable with the second, the third will also be incommensurable with the fourth.

If in a circle which has its diameter rational an equilateral pentagon be inscribed, the side of the pentagon is the irrational straight line called minor.

If, as whole is to whole, so is a number subtracted to a number subtracted, the remainder will also be to the remainder as whole to whole.

If an area be contained by a rational straight line and the fifth binomial, the side of the area is the irrational straight line called the side of a rational plus a medial area.

If an area be contained by a rational straight line and a fifth apotome, the side of the area is a straight line which produces with a rational area a medial whole.

If as many numbers as we please beginning from an unit be in continued proportion, the less measures the greater according to some one of the numbers which have place among the proportional numbers.

A pyramid is a solid figure, contained by planes, which is constructed from one plane to one point.

Alternate ratio means taking the antecedent in relation to the antecedent and the consequent in relation to the consequent.

An acute angle is an angle less than a right angle.

Numbers prime to one another are those which are measured by an unit alone as a common measure.

Similar cones and cylinders are to one another in the triplicate ratio of the diameters in their bases.

To three given straight lines to find a fourth proportional.

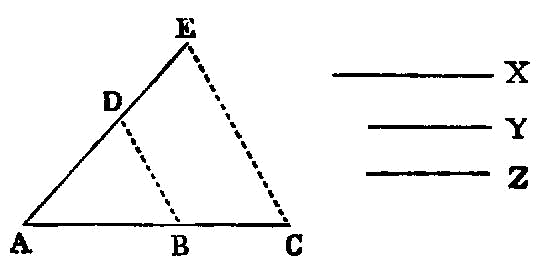
Magnitudes commensurable with the same magnitude are commensurable with one another also.

About a given circle to circumscribe an equilateral and equiangular pentagon.

To a given infinite straight line, from a given point which is not on it, to draw a perpendicular straight line.¹

Between two cube numbers there are two mean proportional numbers, and the cube has to the cube the ratio triplicate of that which the side has to the side.

In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle.

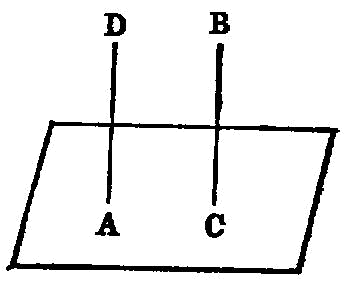
To set up a straight line at right angles to a given plane from a given point in it.

If two circles touch one another externally, the straight line joining their centres will pass through the point of contact.

If as many numbers as we please beginning from an unit be in continued proportion, by however many prime numbers the last is measured, the next to the unit will also be measured by the same.

If any number of magnitudes be proportional, as one of the antecedents is to one of the consequents, so will all the antecedents be to all the consequents.

If there be as many numbers as we please in proportion, then, as one of the antecedents is to one of the consequents, so are all the antecedents to all the consequents.

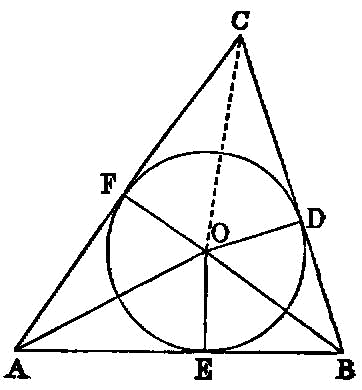
If an equilateral triangle be inscribed in a circle, the square on the side of the triangle is triple of the square on the radius of the circle.

If an area be contained by a rational straight line and the sixth binomial, the side of the area is the irrational straight line called the side of the sum of two medial areas.

If an area be contained by a rational straight line and a sixth apotome, the side of the area is a straight line which produces with a medial area a medial whole.

A prism is a solid figure contained by planes two of which, namely those which are opposite, are equal, similar and parallel, while the rest are parallelograms.

Inverse ratio means taking the consequent as antecedent in relation to the antecedent as consequent.

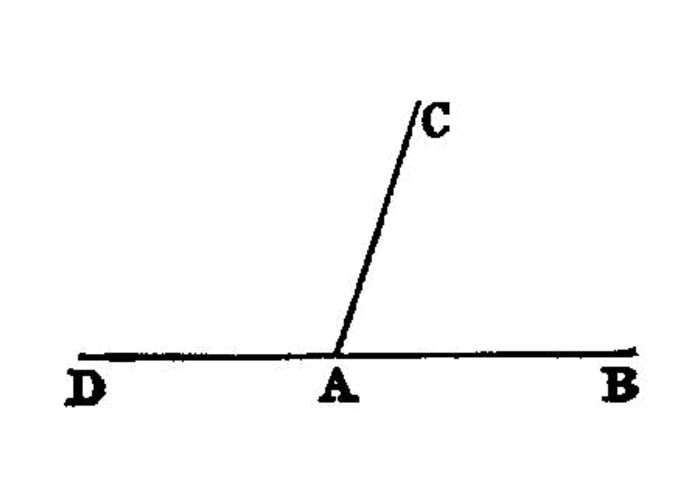
A boundary is that which is an extremity of anything.

A composite number is that which is measured by some number.

To two given straight lines to find a mean proportional.

If a first magnitude have to a second the same ratio as a third to a fourth, and the third have to the fourth a greater ratio than a fifth has to a sixth, the first will also have to the second a greater ratio than the fifth to the sixth.

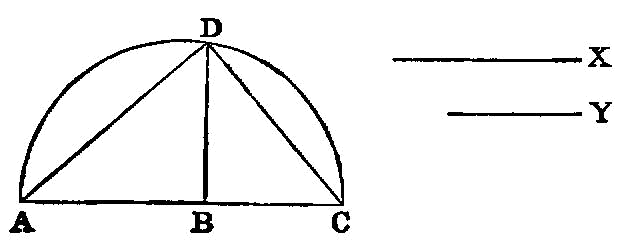
To construct a pyramid, to comprehend it in a given sphere, and to prove that the square on the diameter of the sphere is one and a half times the square on the side of the pyramid.

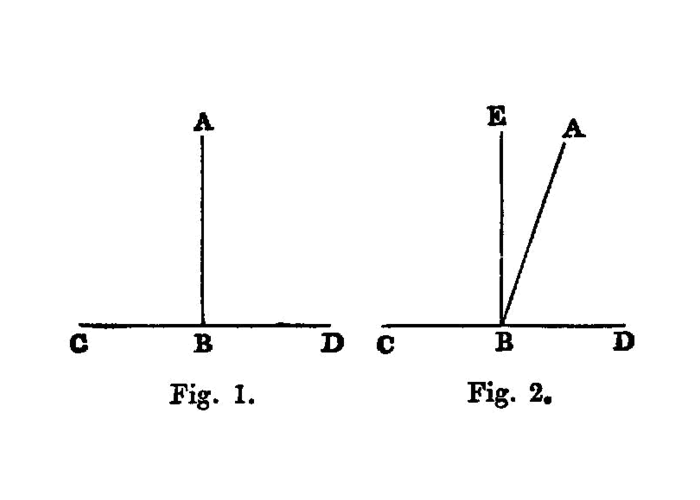
If a straight line set up on a straight line make angles, it will make either two right angles or angles equal to two right angles.

If as many numbers as we please beginning from an unit be in continued proportion, and the number after the unit be prime, the greatest will not be measured by any except those which have a place among the proportional numbers.

If two magnitudes be commensurable, and the one of them be incommensurable with any magnitude, the remaining one will also be incommensurable with the same.

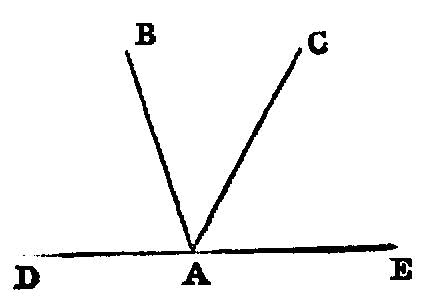
From the same point two straight lines cannot be set up at right angles to the same plane on the same side.

In a given pentagon, which is equilateral and equiangular, to inscribe a circle.

If four numbers be proportional, they will also be proportional alternately.

If a cylinder be cut by a plane which is parallel to its opposite planes, then, as the cylinder is to the cylinder, so will the axis be to the axis.

A circle does not touch a circle at more points than one, whether it touch it internally or externally.

In acute-angled triangles the square on the side subtending the acute angle is less than the squares on the sides containing the acute angle by twice the rectangle contained by one of the sides about the acute angle, namely that on which the perpendicular falls, and the straight line cut off within by the perpendicular towards the acute angle.

If there be as many numbers as we please in continued proportion, and each by multiplying itself make some number, the products will be proportional; and, if the original numbers by multiplying the products make certain numbers, the latter will also be proportional.

The square on the binomial straight line applied to a rational straight line produces as breadth the first binomial.

The square on an apotome applied to a rational straight line produces as breadth a first apotome.

Numbers composite to one another are those which are measured by some number as a common measure.

A figure is that which is contained by any boundary or boundaries.

When, the diameter of a semicircle remaining fixed, the semicircle is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a sphere.

Composition of a ratio means taking the antecedent together with the consequent as one in relation to the consequent by itself.

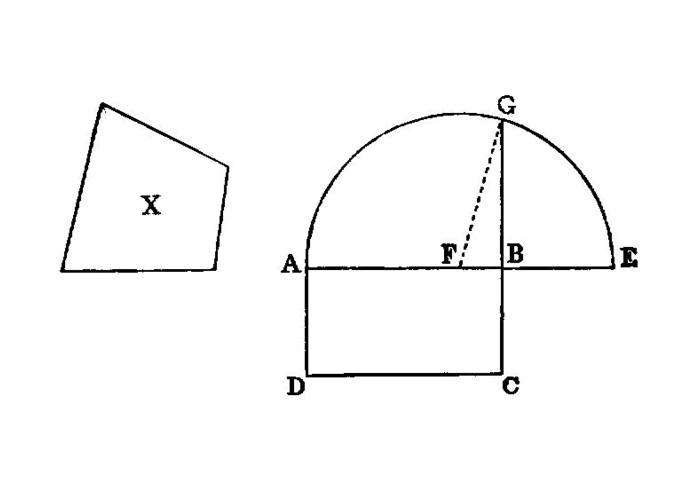
To construct a square equal to a given rectilineal figure.

If a number be the least that is measured by prime numbers, it will not be measured by any other prime number except those originally measuring it.

If there be as many numbers as we please, and others equal to them in multitude, which taken two and two are in the same ratio, they will also be in the same ratio ex aequali.

If a first magnitude have to a second the same ratio as a third has to a fourth, and the first be greater than the third, the second will also be greater than the fourth; if equal, equal; and if less, less.

In a circle equal straight lines are equally distant from the centre, and those which are equally distant from the centre are equal to one another.

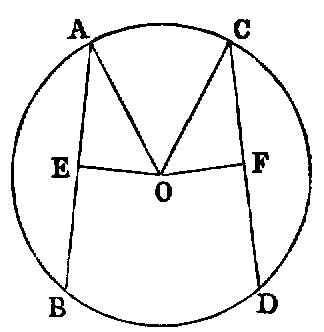
If a square measure a square, the side will also measure the side; and, if the side measure the side, the square will also measure the square.

Planes to which the same straight line is at right angles will be parallel.

About a given pentagon, which is equilateral and equiangular, to circumscribe a circle.

If with any straight line, and at a point on it, two straight lines not lying on the same side make the adjacent angles equal to two right angles, the two straight lines will be in a straight line with one another. ¹

If four straight lines be proportional, and the square on the first be greater than the square on the second by the square on a straight line commensurable with the first, the square on the third will also be greater than the square on the fourth by the square on a straight line commensurable with the third.

In equal and equiangular parallelograms the sides about the equal angles are reciprocally proportional; and equiangular parallelograms in which the sides about the equal angles are reciprocally proportional are equal.

To construct an octahedron and comprehend it in a sphere, as in the preceding case; and to prove that the square on the diameter of the sphere is double of the square on the side of the octahedron.

Cones and cylinders which are on equal bases are to one another as their heights.

The square on the first bimedial straight line applied to a rational straight line produces as breadth the second binomial.

The square on a first apotome of a medial straight line applied to a rational straight line produces as breadth a second apotome.

A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;

Separation of a ratio means taking the excess by which the antecedent exceeds the consequent in relation to the consequent by itself.

A number is said to multiply a number when that which is multiplied is added to itself as many times as there are units in the other, and thus some number is produced.

The axis of the sphere is the straight line which remains fixed and about which the semicircle is turned.

To construct a cube and comprehend it in a sphere, like the pyramid; and to prove that the square on the diameter of the sphere is triple of the square on the side of the cube.

In a given circle to inscribe an equilateral and equiangular hexagon.

If two straight lines meeting one another be parallel to two straight lines meeting one another, not being in the same plane, the planes through them are parallel.

Parts have the same ratio as the same multiples of them taken in corresponding order.

If two commensurable magnitudes be added together, the whole will also be commensurable with each of them; and, if the whole be commensurable with one of them, the original magnitudes will also be commensurable.

Of straight lines in a circle the diameter is greatest, and of the rest the nearer to the centre is always greater than the more remote.

In equal cones and cylinders the bases are reciprocally proportional to the heights; and those cones and cylinders in which the bases are reciprocally proportional to the heights are equal.

In equal triangles which have one angle equal to one angle the sides about the equal angles are reciprocally proportional; and those triangles which have one angle equal to one angle, and in which the sides about the equal angles are reciprocally proportional, are equal.

If two straight lines cut one another, they make the vertical angles ¹ equal to one another.

If three numbers in continued proportion be the least of those which have the same ratio with them, any two whatever added together will be prime to the remaining number.

If an unit measure any number, and another number measure any other number the same number of times, alternately also, the unit will measure the third number the same number of times that the second measures the fourth.

If a cube number measure a cube number, the side will also measure the side; and, if the side measure the side, the cube will also measure the cube.

The square on the second bimedial straight line applied to a rational straight line produces as breadth the third binomial.

The square on a second apotome of a medial straight line applied to a rational straight line produces as breadth a third apotome.

The centre of the sphere is the same as that of the semicircle.

And, when two numbers having multiplied one another make some number, the number so produced is called plane, and its sides are the numbers which have multiplied one another.

And the point is called the centre of the circle.

Conversion of a ratio means taking the antecedent in relation to the excess by which the antecedent exceeds the consequent.

The square on a minor straight line applied to a rational straight line produces as breadth a fourth apotome.

To construct an icosahedron and comprehend it in a sphere, like the aforesaid figures; and to prove that the side of the icosahedron is the irrational straight line called minor.

Given two circles about the same centre, to inscribe in the greater circle an equilateral polygon with an even number of sides which does not touch the lesser circle.

If a square number do not measure a square number, neither will the side measure the side; and, if the side do not measure the side, neither will the square measure the square.

If two numbers by multiplying one another make certain numbers, the numbers so produced will be equal to one another.

If two incommensurable magnitudes be added together, the whole will also be incommensurable with each of them; and, if the whole be incommensurable with one of them, the original magnitudes will also be incommensurable.

In a given circle to inscribe a fifteen-angled figure which shall be both equilateral and equiangular.

The straight line drawn at right angles to the diameter of a circle from its extremity will fall outside the circle, and into the space between the straight line and the circumference another straight line cannot be interposed; further the angle of the semicircle is greater, and the remaining angle less, than any acute rectilineal angle.

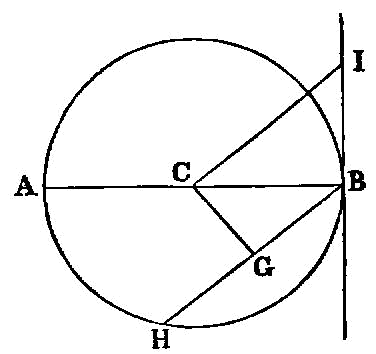
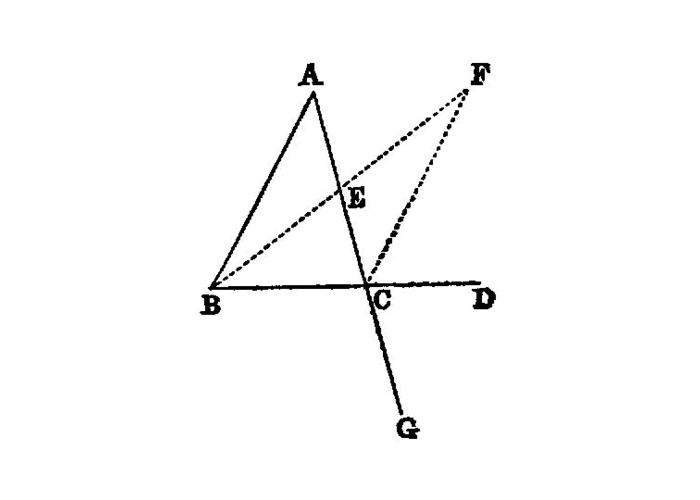
In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles.

If four straight lines be proportional, the rectangle contained by the extremes is equal to the rectangle contained by the means; and, if the rectangle contained by the extremes be equal to the rectangle contained by the means, the four straight lines will be proportional.

If two parallel planes be cut by any plane, their common sections are parallel.

If two numbers be prime to one another, the second will not be to any other number as the first is to the second.

If four magnitudes be proportional, they will also be proportional alternately.

The square on the major straight line applied to a rational straight line produces as breadth the fourth binomial.

A diameter of the sphere is any straight line drawn through the centre and terminated in both directions by the surface of the sphere.

A ratio ex aequali arises when, there being several magnitudes and another set equal to them in multitude which taken two and two are in the same proportion, as the first is to the last among the first magnitudes, so is the first to the last among the second magnitudes;

A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.

And, when three numbers having multiplied one another make some number, the number so produced is solid, and its sides are the numbers which have multiplied one another.

The square on the straight line which produces with a rational area a medial whole, if applied to a rational straight line, produces as breadth a fifth apotome.

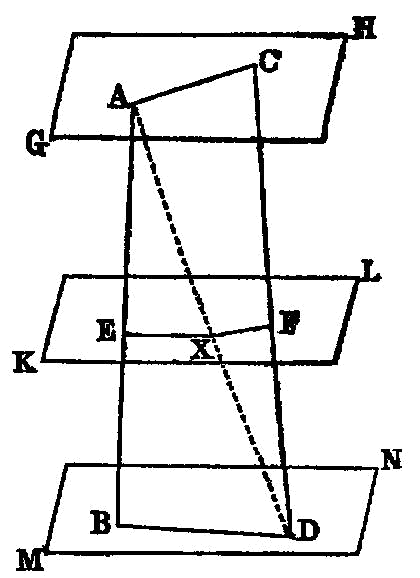
If two straight lines be cut by parallel planes, they will be cut in the same ratios.

To construct a dodecahedron and comprehend it in a sphere, like the aforesaid figures, and to prove that the side of the dodecahedron is the irrational straight line called apotome.

If three straight lines be proportional, the rectangle contained by the extremes is equal to the square on the mean; and, if the rectangle contained by the extremes be equal to the square on the mean, the three straight lines will be proportional.

If there be two unequal straight lines, and to the greater there be applied a parallelogram equal to the fourth part of the square on the less and deficient by a square figure, and if it divide it into parts which are commensurable in length, then the square on the greater will be greater than the square on the less by the square on a straight line commensurable with the greater.

If a cube number do not measure a cube number, neither will the side measure the side; and, if the side do not measure the side, neither will the cube measure the cube.

If a number by multiplying two numbers make certain numbers, the numbers so produced will have the same ratio as the numbers multiplied.

If magnitudes be proportional componendo, they will also be proportional separando.

If there be as many numbers as we please in continued proportion, and the extremes of them be prime to one another, the last will not be to any other number as the first to the second.

Given two spheres about the same centre, to inscribe in the greater sphere a polyhedral solid which does not touch the lesser sphere at its surface.

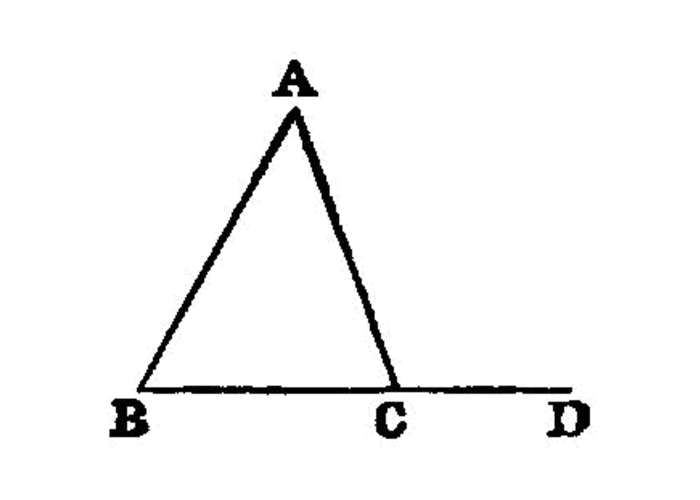
In any triangle two angles taken together in any manner ¹ are less than two right angles.

From a given point to draw a straight line touching a given circle.

The square on the side of a rational plus a medial area applied to a rational straight line produces as breadth the fifth binomial.

When, one side of those about the right angle in a right-angled triangle remaining fixed, the triangle is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cone.

A perturbed proportion arises when, there being three magnitudes and another set equal to them in multitude, as antecedent is to consequent among the first magnitudes, so is antecedent to consequent among the second magnitudes, while, as the consequent is to a third among the first magnitudes, so is a third to the antecedent among the second magnitudes.

A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.

A square number is equal multiplied by equal, or a number which is contained by two equal numbers.

The square on the straight line which produces with a medial area a medial whole, if applied to a rational straight line, produces as breadth a sixth apotome.

In any triangle the greater side subtends the greater angle.

Given two numbers, to investigate whether it is possible to find a third proportional to them.

On a given straight line to describe a rectilineal figure similar and similarly situated to a given rectilineal figure.

Spheres are to one another in the triplicate ratio of their respective diameters.

If there be two unequal straight lines, and to the greater there be applied a parallelogram equal to the fourth part of the square on the less and deficient by a square figure, and if it divide it into parts which are incommensurable, the square on the greater will be greater than the square on the less by the square on a straight line incommensurable with the greater.

Between two similar plane numbers there is one mean proportional number; and the plane number has to the plane number the ratio duplicate of that which the corresponding side has to the corresponding side.

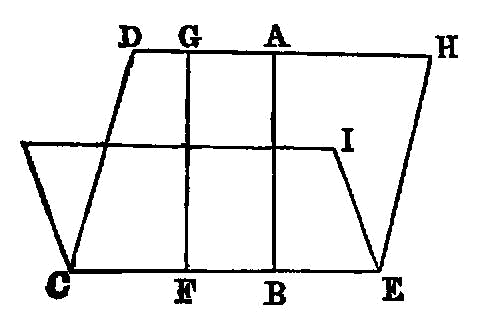
If a straight line be at right angles to any plane, all the planes through it will also be at right angles to the same plane.

If a straight line touch a circle, and a straight line be joined from the centre to the point of contact, the straight line so joined will be perpendicular to the tangent.

If magnitudes be proportional separando, they will also be proportional componendo.

If two numbers by multiplying any number make certain numbers, the numbers so produced will have the same ratio as the multipliers.

To set out the sides of the five figures and to compare them with one another.

The square on the side of the sum of two medial areas applied to a rational straight line produces as breadth the sixth binomial.

And a cube is equal multiplied by equal and again by equal, or a number which is contained by three equal numbers.

The axis of the cone is the straight line which remains fixed and about which the triangle is turned.

A straight line commensurable in length with an apotome is an apotome and the same in order.

If four numbers be proportional, the number produced from the first and fourth will be equal to the number produced from the second and third; and, if the number produced from the first and fourth be equal to that produced from the second and third, the four numbers will be proportional.

Similar triangles are to one another in the duplicate ratio of the corresponding sides.

Given three numbers, to investigate when it is possible to find a fourth proportional to them.

In any triangle the greater angle is subtended by the greater side.

If two planes which cut one another be at right angles to any plane, their common section will also be at right angles to the same plane.

If a straight line touch a circle, and from the point of contact a straight line be drawn at right angles to the tangent, the centre of the circle will be on the straight line so drawn.

The rectangle contained by rational straight lines commensurable in length is rational.

Between two similar solid numbers there fall two mean proportional numbers; and the solid number has to the similar solid number the ratio triplicate of that which the corresponding side has to the corresponding side.

If, as a whole is to a whole, so is a part subtracted to a part subtracted, the remainder will also be to the remainder as whole to whole.

A straight line commensurable in length with a binomial straight line is itself also binomial and the same in order.

Numbers are proportional when the first is the same multiple, or the same part, or the same parts, of the second that the third is of the fourth.

And the base is the circle described by the straight line which is carried round.

Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.

A straight line commensurable with an apotome of a medial straight line is an apotome of a medial straight line and the same in order.

The least numbers of those which have the same ratio with them measure those which have the same ratio the same number of times, the greater the greater and the less the less.

In a circle the angle at the centre is double of the angle at the circumference, when the angles have the same circumference as base.

If a solid angle be contained by three plane angles, any two, taken together in any manner, are greater than the remaining one.

If there be three magnitudes, and others equal to them in multitude, which taken two and two are in the same ratio, and if ex aequali the first be greater than the third, the fourth will also be greater than the sixth; if equal, equal; and, if less, less.

If one mean proportional number fall between two numbers, the numbers will be similar plane numbers.

Prime numbers are more than any assigned multitude of prime numbers.

If a rational area be applied to a rational straight line, it produces as breadth a straight line rational and commensurable in length with the straight line to which it is applied.

Similar polygons are divided into similar triangles, and into triangles equal in multitude and in the same ratio as the wholes, and the polygon has to the polygon a ratio duplicate of that which the corresponding side has to the corresponding side.

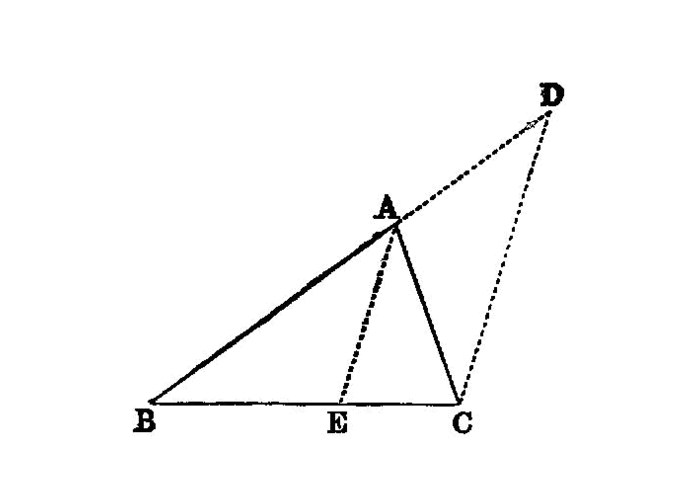
In any triangle two sides taken together in any manner are greater than the remaining one. ¹

A straight line commensurable in length with a bimedial straight line is itself also bimedial and the same in order.

Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute angled triangle that which has its three angles acute.

Similar plane and solid numbers are those which have their sides proportional.

When, one side of those about the right angle in a rectangular parallelogram remaining fixed, the parallelogram is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cylinder.

A straight line commensurable with a minor straight line is minor.

If on one of the sides of a triangle, from its extremities, there be constructed two straight lines meeting within the triangle,¹ the straight lines so constructed ² will be less than the remaining two sides of the triangle, but will contain a greater angle.

In a circle the angles in the same segment are equal to one another.

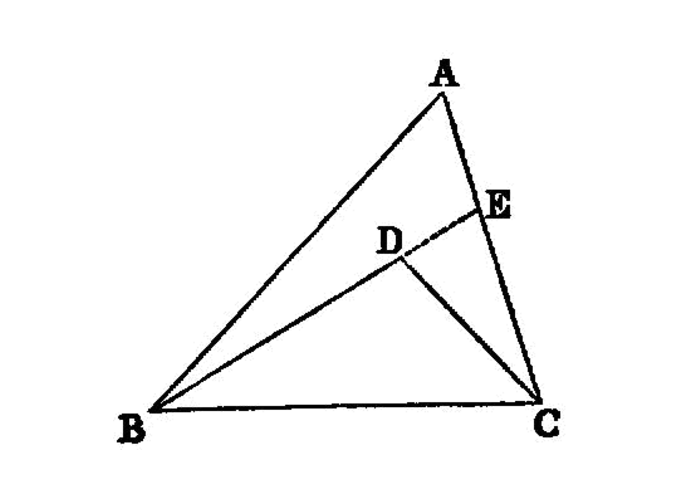
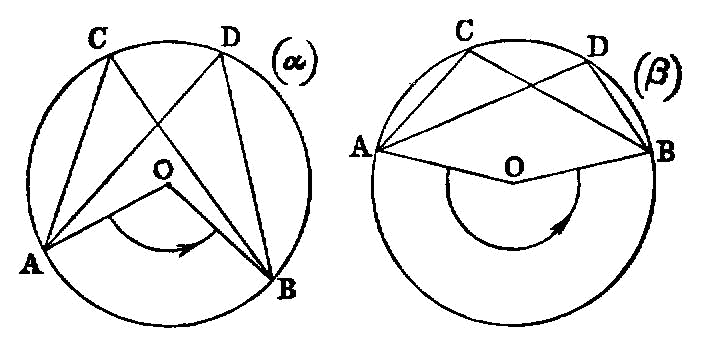
The rectangle contained by rational straight lines commensurable in square only is irrational, and the side of the square equal to it is irrational. Let the latter be called medial.

Figures which are similar to the same rectilineal figure are also similar to one another.

If as many even numbers as we please be added together, the whole is even.

If two mean proportional numbers fall between two numbers, the numbers are similar solid numbers.

Any solid angle is contained by plane angles less than four right angles.

Numbers prime to one another are the least of those which have the same ratio with them.

If there be three magnitudes, and others equal to them in multitude, which taken two and two together are in the same ratio, and the proportion of them be perturbed, then, if ex aequali the first magnitude is greater than the third, the fourth will also be greater than the sixth; if equal, equal; and if less, less.

A straight line commensurable with a major straight line is itself also major.

A perfect number is that which is equal to its own parts.

Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.

The axis of the cylinder is the straight line which remains fixed and about which the parallelogram is turned.

A straight line commensurable with that which produces with a rational area a medial whole is a straight line which produces with a rational area a medial whole.

Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it is necessary ¹ that two of the straight lines taken together in any manner should be greater than the remaining one. [I.20] ^{2 3}

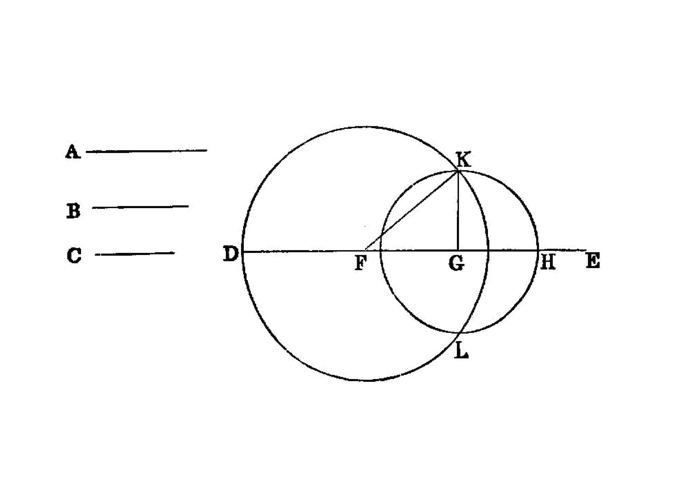
If there be three plane angles of which two, taken together in any manner, are greater than the remaining one, and they are contained by equal straight lines, it is possible to construct a triangle out of the straight lines joining the extremities of the equal straight lines.

If there be any number of magnitudes whatever, and others equal to them in multitude, which taken two and two together are in the same ratio, they will also be in the same ratio ex aequali.

If three numbers be in continued proportion, and the first be square, the third will also be square.

The square on a medial straight line, if applied to a rational straight line, produces as breadth a straight line rational and incommensurable in length with that to which it is applied.

The least numbers of those which have the same ratio with them are prime to one another.

If four straight lines be proportional, the rectilineal figures similar and similarly described upon them will also be proportional; and, if the rectilineal figures similar and similarly described upon them be proportional, the straight lines will themselves also be proportional.

The opposite angles of quadrilaterals in circles are equal to two right angles.

If as many odd numbers as we please be added together, and their multitude be even, the whole will be even.

A straight line commensurable with the side of a rational plus a medial area is itself also the side of a rational plus a medial area.

And the bases are the circles described by the two sides opposite to one another which are carried round.

Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.

A straight line commensurable with that which produces with a medial area a medial whole is itself also a straight line which produces with a medial area a medial whole.

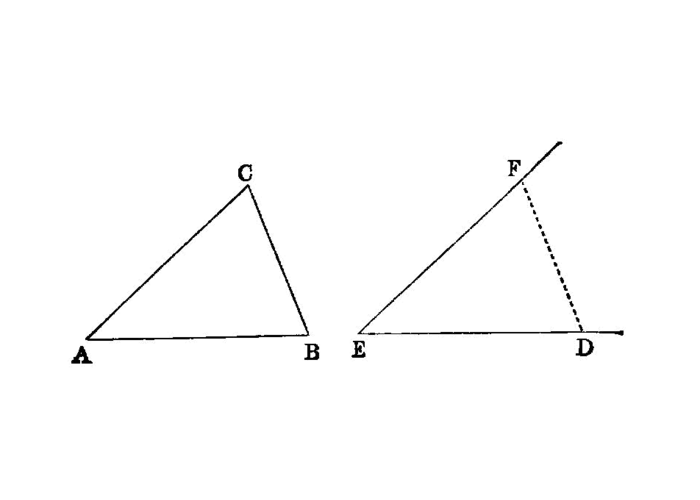
On a given straight line and at a point on it to construct a rectilineal angle equal to a given rectilineal angle.

To construct a solid angle out of three plane angles two of which, taken together in any manner, are greater than the remaining one: thus the three angles must be less than four right angles.

If two number be prime to one another, the number which measures the one of them will be prime to the remaining number.

If as many odd numbers as we please be added together, and their multitude be odd, the whole will also be odd.

If there be three magnitudes, and others equal to them in multitude, which taken two and two together are in the same ratio, and the proportion of them be perturbed, they will also be in the same ratio ex aequali.

If four numbers be in continued proportion, and the first be cube, the fourth will also be cube.

Equiangular parallelograms have to one another the ratio compounded of the ratios of their sides.

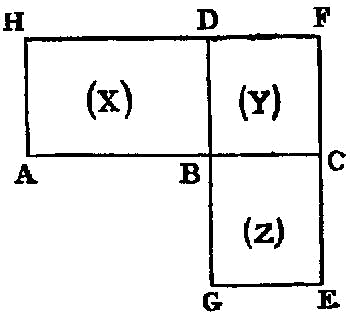
A straight line commensurable with a medial straight line is medial.

On the same straight line there cannot be constructed two similar and unequal segments of circles on the same side.

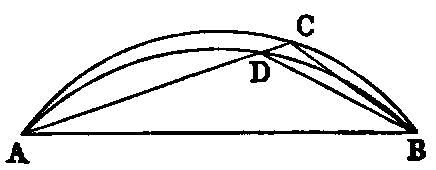
A straight line commensurable with the side of the sum of two medial areas is the side of the sum of two medial areas.

Similar cones and cylinders are those in which the axes and the diameters of the bases are proportional.

If from a rational area a medial area be subtracted, the side of the remaining area becomes one of two irrational straight lines, either an apotome or a minor straight line.

If a solid be contained by parallel planes, the opposite planes in it are equal and parallelogrammic.

If from an even number an even number be subtracted, the remainder will be even.

If a first magnitude have to a second the same ratio as a third has to a fourth, and also a fifth have to the second the same ratio as a sixth to the fourth, the first and fifth added together will have to the second the same ratio as the third and sixth have to the fourth.

Similar segments of circles on equal straight lines are equal to one another.

If two numbers have to one another the ratio which a square number has to a square number, and the first be square, the second will also be square.

If two numbers be prime to any number, their product also will be prime to the same.

In any parallelogram the parallelograms about the diameter are similar both to the whole and to one another.

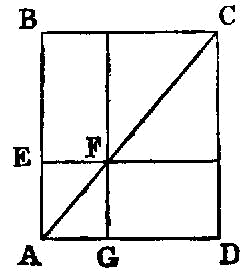
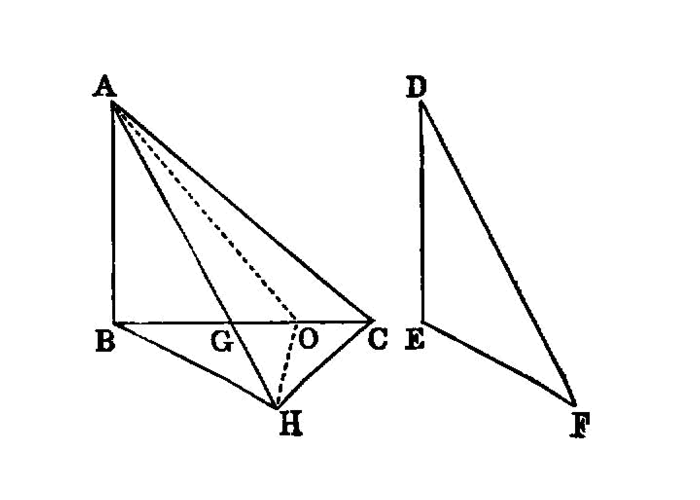
If two triangles have the two sides equal to two sides respectively, but have the one of the angles contained by the equal straight lines greater than the other, they will also have the base greater than the base.

The rectangle contained by medial straight lines commensurable in length is medial.

If a rational and a medial area be added together, four irrational straight lines arise, namely a binomial or a first bimedial or a major or a side of a rational plus a medial area.

A cube is a solid figure contained by six equal squares.

If from a medial area a rational area be subtracted, there arise two other irrational straight lines, either a first apotome of a medial straight line or a straight line which produces with a rational area a medial whole.

The rectangle contained by medial straight lines commensurable in square only is either rational or medial.

If a parallelepipedal solid be cut by a plane which is parallel to the opposite planes, then, as the base is to the base, so will the solid be to the solid.

To construct one and the same figure similar to a given rectilineal figure and equal to another given rectilineal figure.

If two numbers have to one another the ratio which a cube number has to a cube number, and the first be cube, the second will also be cube.

If from an even number an odd number be subtracted, the remainder will be odd.

If four magnitudes be proportional, the greatest and the least are greater than the remaining two.

Given a segment of a circle, to describe the complete circle of which it is a segment.

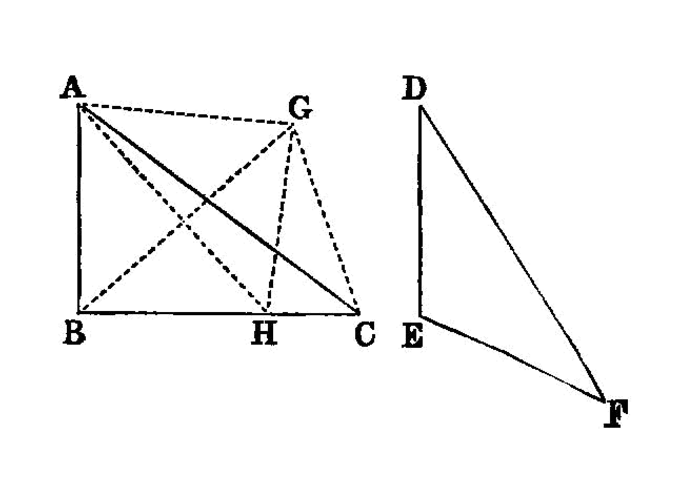
If two triangles have the two sides equal to two sides respectively, but have the base greater than the base, they will also have the one of the angles contained by the equal straight lines greater than the other.

If two numbers be prime to one another, the product of one of them into itself will be prime to the remaining one.

If two medial areas incommensurable with one another be added together, the remaining two irrational straight lines arise, namely either a second bimedial or a side of the sum of two medial areas.

An octahedron is a solid figure contained by eight equal and equilateral triangles.

If from a medial area there be subtracted a medial area incommensurable with the whole, the two remaining irrational straight lines arise, either a second apotome of a medial straight line or a straight line which produces with a medial area a medial whole.

On a given straight line, and at a given point on it, to construct a solid angle equal to a given solid angle.

If two triangles have the two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, ¹ or that subtending one of the equal angles, they will also have the remaining sides equal to the remaining sides and the remaining angle to the remaining angle.

If from an odd number an odd number be subtracted, the remainder will be even.

4 medial area does not exceed a medial area by a rational area.

In equal circles equal angles stand on equal circumferences, whether they stand at the centres or at the circumferences.

If from a parallelogram there be taken away a parallelogram similar and similarly situated to the whole and having a common angle with it, it is about the same diameter with the whole

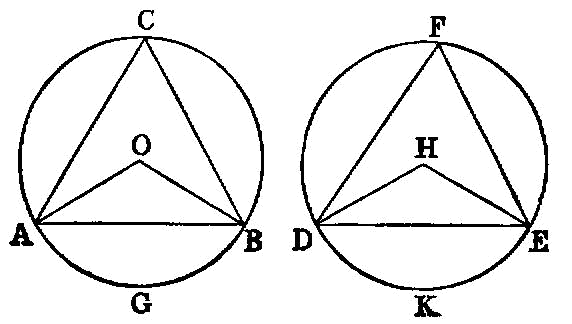
If two numbers be prime to two numbers, both to each, their products also will be prime to one another.

Similar plane numbers have to one another the ratio which a square number has to a square number.

If from a rational straight line there be subtracted a rational straight line commensurable with the whole in square only, the remainder is irrational; and let it be called an apotome.

An icosahedron is a solid figure contained by twenty equal and equilateral triangles.

The apotome is not the same with the binomial straight line.

Similar solid numbers have to one another the ratio which a cube number has to a cube number.

If two numbers be prime to one another, and each by multiplying itself make a certain number, the products will be prime to one another; and, if the original numbers by multiplying the products make certain numbers, the latter will also be prime to one another [and this is always the case with the extremes].

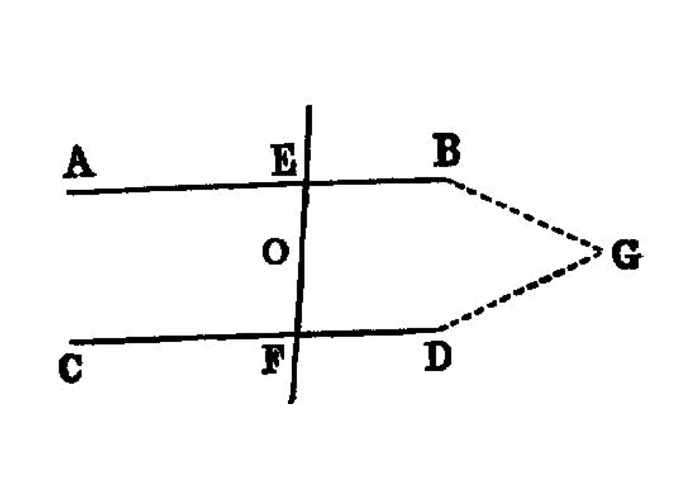
If a straight line falling on two straight lines ¹ make the alternate angles [^I.27:2] equal to one another, the straight lines will be parallel to one another.

If from an odd number an even number be subtracted, the remainder will be odd.

To find medial straight lines commensurable in square only which contain a rational rectangle.

In equal circles angles standing on equal circumferences are equal to one another, whether they stand at the centres or at the circumferences.

On a given straight line to describe a parallelepipedal solid similar and similarly situated to a given parallelepipedal solid.

Of all the parallelograms applied to the same straight line and deficient by parallelogrammic figures similar and similarly situated to that described on the half of the straight line, that parallelogram is greatest which is applied to the half of the straight line and is similar to the defect.

If from a medial straight line there be subtracted a medial straight line which is commensurable with the whole in square only, and which contains with the whole a rational rectangle, the remainder is irrational. And let it be called a first apotome of a medial straight line.

A dodecahedron is a solid figure contained by twelve equal, equilateral, and equiangular pentagons.

The square on a rational straight line applied to the binomial straight line produces as breadth an apotome the terms of which are commensurable with the terms of the binomial and moreover in the same ratio; and further the apotome so arising will have the same order as the binomial straight line.

To a given straight line to apply a parallelogram equal to a given rectilineal figure and deficient by a parallelogrammic figure similar to a given one : thus the given rectilineal figure must not be greater than the parallelogram described on the half of the straight line and similar to the defect.

If a parallelepipedal solid be cut by a plane through the diagonals of the opposite planes, the solid will be bisected by the plane.

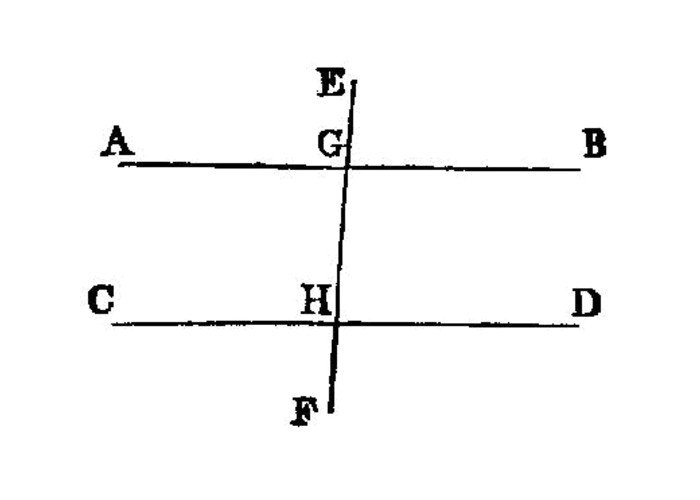
If a straight line falling on two straight lines make the exterior angle equal to the interior and opposite angle on the same side, or the interior angles on the same side equal to two right angles, the straight lines will be parallel to one another.

If two numbers be prime to one another, the sum will also be prime to each of them; and, if the sum of two numbers be prime to any one of them, the original numbers will also be prime to one another.

In equal circles equal straight lines cut off equal circumferences, the greater equal to the greater and the less to the less.

To find medial straight lines commensurable in square only which contain a medial rectangle.

If an odd number by multiplying an even number make some number, the product will be even.

If from a medial straight line there be subtracted a medial straight line which is commensurable with the whole in square only, and which contains with the whole a medial rectangle, the remainder is irrational; and let it be called a second apotome of a medial straight line.

The square on a rational straight line, if applied to an apotome, produces as, breadth the binomial straight line the terms of which are commensurable with the terms of the apotome and in the same ratio; and further the binomial so arising has the same order as the apotome.

If an odd number by multiplying an odd number make some number, the product will be odd.

Parallelepipedal solids which are on the same base and of the same height, and in which the extremities of the sides which stand up are on the same straight lines, are equal to one another.

Any prime number is prime to any number which it does not measure.

To a given straight line to apply a parallelogram equal to a given rectilineal figure and exceeding by a parallelogrammic figure similar to a given one.

In equal circles equal circumferences are subtended by equal straight lines.

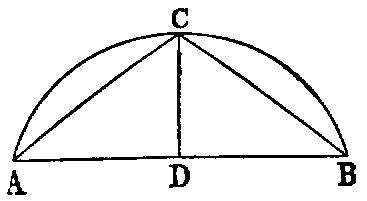
To find two rational straight lines commensurable in square only and such that the square on the greater is greater than the square on the less by the square on a straight line commensurable in length with the greater.

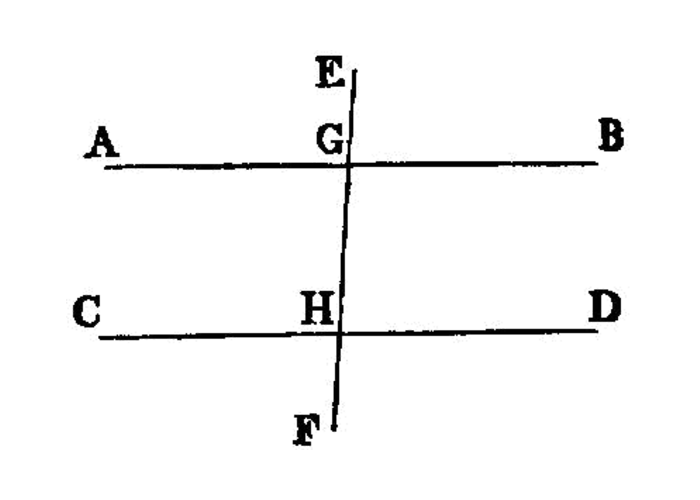
A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the interior angles on the same side equal to two right angles.

If from a straight line there be subtracted a straight line which is incommensurable in square with the whole and which with the whole makes the squares on them added together rational, but the rectangle contained by them medial, the remainder is irrational; and let it be called minor.

If an area be contained by an apotome and the binomial straight line the terms of which are commensurable with the terms of the apotome and in the same ratio, the side of the area is rational.

Parallelepipedal solids which are on the same base and of the same height, and in which the extremities of the sides which stand up are not on the same straight lines, are equal to one another.

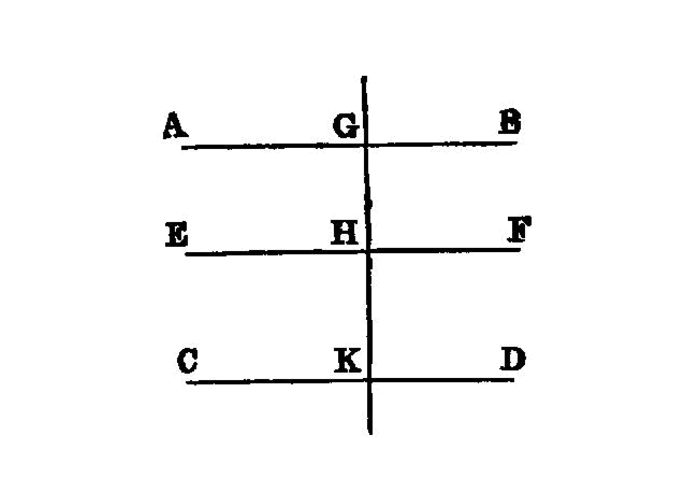
Straight lines parallel to the same straight line are also parallel to one another.

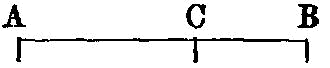
To cut a given finite straight line in extreme and mean ratio.

If two numbers by multiplying one another make some number, and any prime number measure the product, it will also measure one of the original numbers.

To bisect a given circumference.

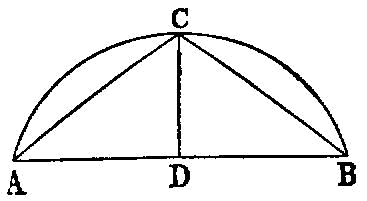
To find two rational straight lines commensurable in square only and such that the square on the greater is greater is greater than the square on the less by the square on a straight line incommensurable in length with the greater.

If an odd number measure an even number, it will also measure the half of it.

If from a straight line there be subtracted a straight line which is incommensurable in square with the whole, and which with the whole makes the sum of the squares on them medial, but twice the rectangle contained by them rational, the remainder is irrational: and let it be called that which produces with a rational area a medial whole.

From a medial straight line there arise irrational straight lines infinite in number, and none of them is the same as any of the preceding.

To find two medial straight lines commensurable in square only, containing a rational rectangle, and such that the square on the greater is greater than the square on the less by the square on a straight line commensurable in length with the greater.

In a circle the angle in the semicircle is right, that in a greater segment less than a right angle, and that in a less segment greater than a right angle; and further the angle of the greater segment is greater than a right angle, and the angle of the less segment less than a right angle.

Through a given point to draw a straight line parallel to a given straight line.

Parallelepipedal solids which are on equal bases and of the same height are equal to one another.

Any composite number is measured by some prime number.

In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.

If an odd number be prime to any number, it will also be prime to the double of it.

If from a straight line there be subtracted a straight line which is incommensurable in square with the whole and which with the whole makes the sum of the squares on them medial, twice the rectangle contained by them medial, and further the squares on them incommensurable with twice the rectangle contained by them, the remainder is irrational; and let it be called that which produces with a medial area a medial whole.

If a straight line touch a circle, and from the point of contact there be drawn across, in the circle, a straight line cutting the circle, the angles which it makes with the tangent will be equal to the angles in the alternate segments of the circle.

If two triangles having two sides proportional to two sides be placed together at one angle so that their corresponding sides are also parallel, the remaining sides of the triangles will be in a straight line.

Each of the numbers which are continually doubled beginning from a dyad is even-times even only.

Parallelepipedal solids which are of the same height are to one another as their bases.

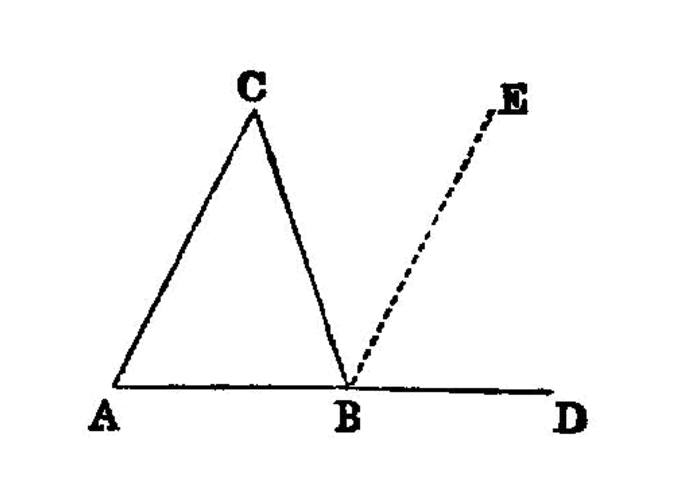
In any triangle, if one of the sides be produced, the exterior angle is equal to the two interior and opposite angles, and the three interior angles of the triangle are equal to two right angles.

To find two medial straight lines commensurable in square only, containing a medial rectangle, and such that the square on the greater is greater than the square on the less by the square on a straight line commensurable with the greater.

Any number either is prime or is measured by some prime number.

To an apotome only one rational straight line can be annexed which is commensurable with the whole in square only.

The straight lines joining equal and parallel straight lines (at the extremities which are) in the same directions (respectively) [^I.33:1] are themselves also equal and parallel.

Given as many numbers as we please, to find the least of those which have the same ratio with them.

Similar parallelepipedal solids are to one another in the triplicate ratio of their corresponding sides.

In equal circles angles have the same ratio as the circumferences on which they stand, whether they stand at the centres or at the circumferences.

To find two straight lines incommensurable in square which make the sum of the squares on them rational but the rectangle contained by them medial.

If a number have its half odd, it is even-times odd only.

On a given straight line to describe a segment of a circle admitting an angle equal to a given rectilineal angle.

To a first apotome of a medial straight line only one medial straight line can be annexed which is commensurable with the whole in square only and which contains with the whole a rational rectangle.

From a given circle to cut off a segment admitting an angle equal to a given rectilineal angle.

Given two numbers, to find the least number which they measure.

If a number neither be one of those which are continually doubled from a dyad, nor have its half odd, it is both eventimes even and even-times odd.

To find two straight lines incommensurable in square which make the sum of the squares on them medial but the rectangle contained by them rational.

In equal parallelepipedal solids the bases are reciprocally proportional to the heights; and those parallelepipedal solids in which the bases are reciprocally proportional to the heights are equal.

In parallelogrammic areasi ¹ the opposite sides and angles are equal to one another, and the diameter bisects the areas.

To a second apotome of a medial straight line only one medial straight line can be annexed which is commensurable with the whole in square only and which contains with the whole a medial rectangle.

If there be two equal plane angles, and on their vertices there be set up elevated straight lines containing equal angles with the original straight lines respectively, if on the elevated straight lines points be taken at random and perpendiculars be drawn from them to the planes in which the original angles are, and if from the points so arising in the planes straight lines be joined to the vertices of the original angles, they will contain, with the elevated straight lines, equal angles.

If two numbers measure any number, the least number measured by them will also measure the same.

If in a circle two straight lines cut one another, the rectangle contained by the segments of the one is equal to the rectangle contained by the segments of the other.

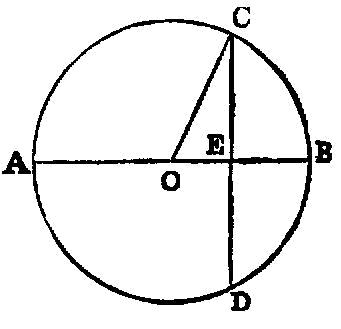
To find two straight lines incommensurable in square which make the sum of the squares on them medial and the rectangle contained by them medial and moreover incommensurable with the sum of the squares on them.

Parallelograms which are on the same base and in the same parallels are equal to one another.

If as many numbers as we please be in continued proportion, and there be subtracted from the second and the last numbers equal to the first, then, as the excess of the second is to the first, so will the excess of the last be to all those before it.

To a minor straight line only one straight line can be annexed which is incommensurable in square with the whole and which makes, with the whole, the sum of the squares on them rational but twice the rectangle contained by them medial.

Given three numbers, to find the least number which they measure.

Parallelograms which are on equal bases and in the same parallels are equal to one another.

If a point be taken outside a circle and from it there fall on the circle two straight lines, and if one of them cut the circle and the other touch it, the rectangle contained by the whole of the straight line which cuts the circle and the straight line intercepted on it outside between the point and the convex circumference will be equal to the square on the tangent.

If two rational straight lines commensurable in square only be added together, the whole is irrational; and let it be called binomial.

If as many numbers as we please beginning from an unit be set out continuously in double proportion, until the sum of all becomes prime, and if the sum multiplied into the last make some number, the product will be perfect.

If three straight lines be proportional, the parallelepipedal solid formed out of the three is equal to the parallelepipedal solid on the mean which is equilateral, but equiangular with the aforesaid solid.

To a straight line which produces with a rational area a medial whole only one straight line can be annexed which is incommensurable in square with the whole straight line and which with the whole straight line makes the sum of the squares on them medial, but twice the rectangle contained by them rational.

If a number be measured by any number, the number which is measured will have a part called by the same name as the measuring number.

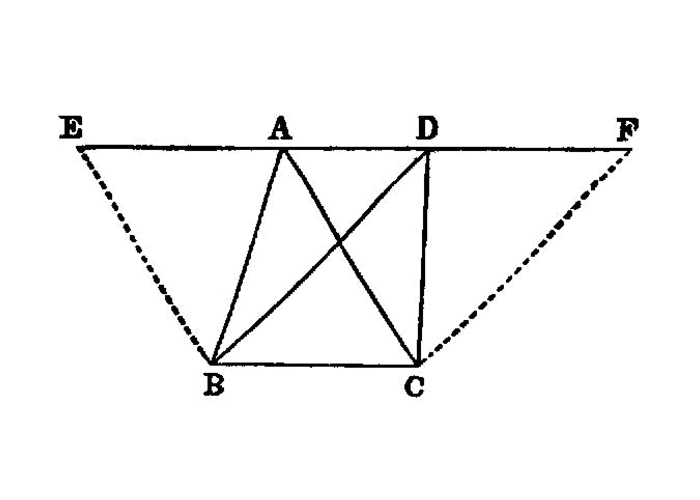
Triangles which are on the same base and in the same parallels are equal to one another.

If four straight lines be proportional, the parallelepipedal solids on them which are similar and similarly described will also be proportional; and, if the parallelepipedal solids on them which are similar and similarly described be proportional, the straight lines will themselves also be proportional.

If a point be taken outside a circle and from the point there fall on the circle two straight lines, if one of them cut the circle, and the other fall on it, and if further the rectangle contained by the whole of the straight line which cuts the circle and the straight line intercepted on it outside between the point and the convex circumference be equal to the square on the straight line which falls on the circle, the straight line which falls on it will touch the circle.

If two medial straight lines commensurable in square only and containing a rational rectangle be added together, the whole is irrational; and let it be called a first bimedial straight line.

To a straight line which produces with a medial area a medial whole only one straight line can be annexed which is incommensurable in square with the whole straight line and which with the whole straight line makes the sum of the squares on them medial and twice the rectangle contained by them both medial and also incommensurable with the sum of the squares on them.

If a number have any part whatever, it will be measured by a number called by the same name as the part.

Triangles which are on equal bases and in the same parallels are equal to one another.

If the sides of the opposite planes of a cube be bisected, and planes be carried through the points of section, the common section of the planes and the diameter of the cube bisect one another.

If two medial straight lines commensurable in square only and containing a medial rectangle be added together, the whole is irrational; and let it be called a second bimedial straight line.

If there be two prisms of equal height, and one have a parallelogram as base and the other a triangle, and if the parallelogram be double of the triangle, the prisms will be equal.

To find the number which is the least that will have given parts.

Equal triangles which are on the same base and on the same side are also in the same parallels.

If two straight lines incommensurable in square which make the sum of the squares on them rational, but the rectangle contained by them medial, be added together, the whole straight line is irrational : and let it be called major.

If two straight lines incommensurable in square which make the sum of the squares on them medial, but the rectangle contained by them rational, be added together, the whole straight line is irrational; and let it be called the side of a rational plus a medial area.

Equal triangles which are on equal bases and on the same side are also in the same parallels

If two straight lines incommensurable in square which make the sum of the squares on them medial, and the rectangle contained by them medial and also incommensurable with the sum of the squares on them, be added together, the whole straight line is irrational; and let it be called the side of the sum of two medial areas.

If a parallelogram have the same base with a triangle and be in the same parallels, the parallelogram is double of the triangle.

A binomial straight line is divided into its terms at one point only.

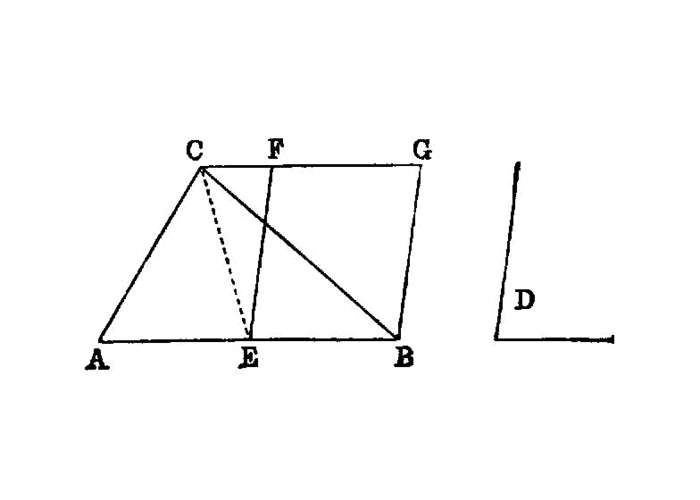
To construct, in a given rectilineal angle, a parallelogram equal to a given triangle.

A first bimedial straight line is divided at one point only.

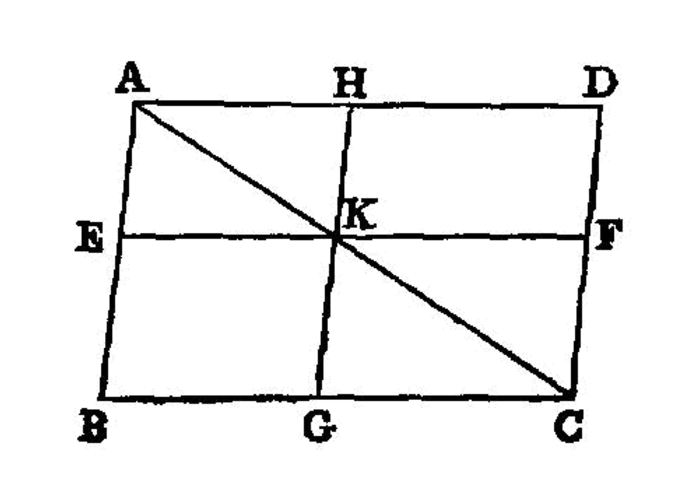
In any parallelogram the complements ¹ of the parallelograms about the diameter are equal to one another.

A second bimedial straight line is divided at one point only.

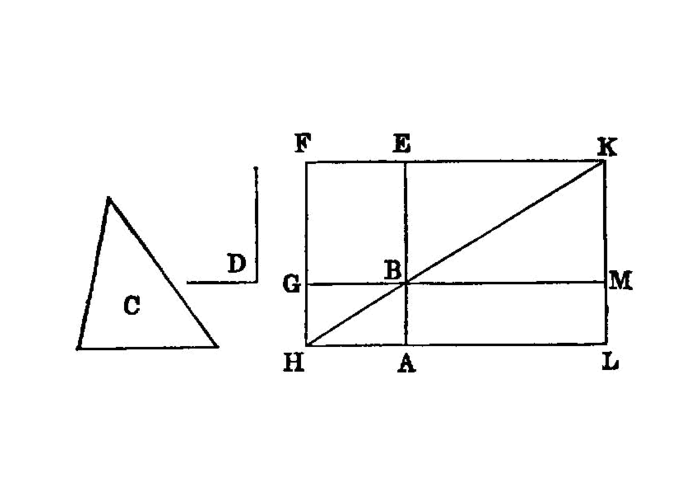
To a given straight line to apply, in a given rectilineal angle, a parallelogram equal to a given triangle.

A major straight line is divided at one and the same point only.

To construct, in a given rectilineal angle, a parallelogram equal to a given rectilineal figure.

The side of a rational plus a medial area is divided at one point only.

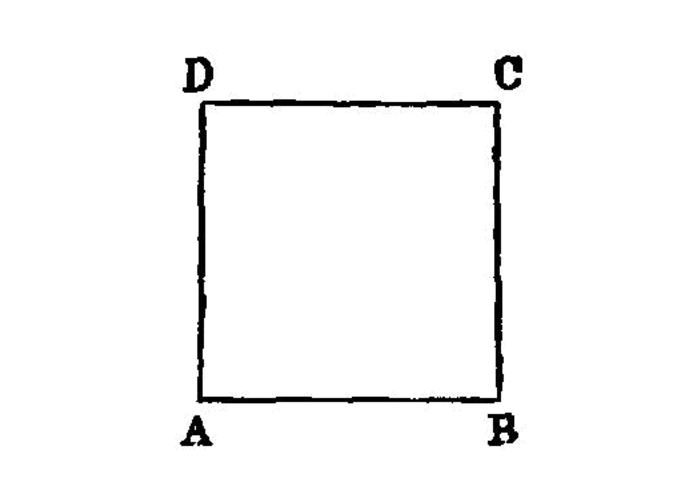
On a given straight line to describe a square.

The side of the sum of two medial areas is divided at one point only.

In right-angled triangles the square on ¹ the side subtending the right angle ² is equal to the squares on the sides containing the right angle.

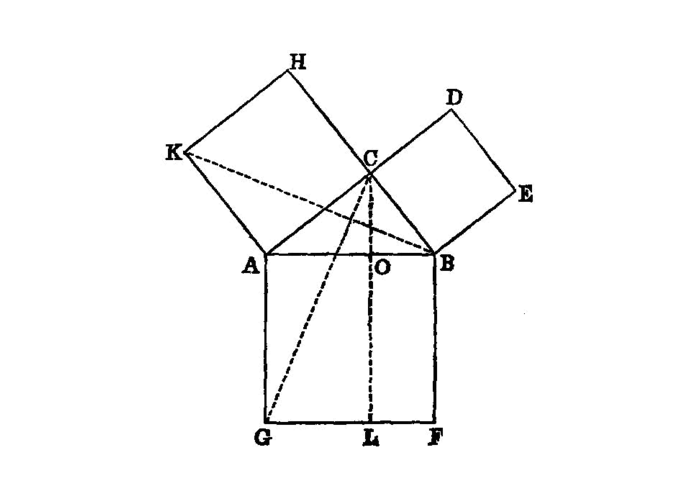
If in a triangle the square on one of the sides be equal to the squares on the remaining two sides of the triangle, the angle contained by the remaining two sides of the triangle is right.